逆数の意味と求め方を分かりやすく解説

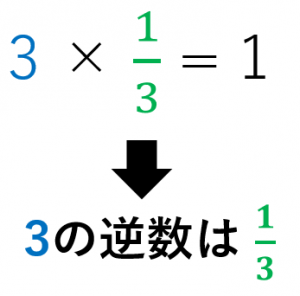
具体例

他にも、逆数の例をたくさん挙げてみます。

ある数	その逆数	確認の計算
$3$	$\dfrac{1}{3}$	$3\times\dfrac{1}{3}=1$
$0.2$	$5$	$0.2\times 5=1$
$1$	$1$	$1\times 1=1$
$-\dfrac{1}{2}$	$-2$	$\left(-\dfrac{1}{2}\right)\times (-1)=1$
$0$	なし	$0$ とかけ算して $0$ になる数字はありません

このページでは、
・整数の逆数
・分数の逆数
・小数の逆数
の求め方をそれぞれ見ていきます。

整数の逆数の求め方

例えば、$3$ の逆数は $\dfrac{1}{3}$ です。

問題

(1) $5$ の逆数を計算せよ。
(2) $334$ の逆数を計算せよ。

答え

(1) $5$ の逆数は、$\dfrac{1}{5}$ です。
実際、$5\times \dfrac{1}{5}=1$ となっています。

(2) $334$ の逆数は、$\dfrac{1}{334}$ です。
実際、$334\times \dfrac{1}{334}=1$ となっています。

分数の逆数の求め方

$\dfrac{n}{m}\times\dfrac{m}{n}=1$ だからです（→分数のかけ算）。

問題

(3) $\dfrac{2}{3}$ の逆数を計算せよ。
(4) $\dfrac{1}{39}$ の逆数を計算せよ。

答え

(3) $\dfrac{2}{3}$ の逆数は、$\dfrac{3}{2}$

(4) $\dfrac{1}{39}$ の逆数は、$\dfrac{39}{1}=39$

小数の逆数の求め方

問題

(5) $0.3$ の逆数を計算せよ。
(6) $-0.29$ の逆数を計算せよ。

答え

(5) $0.3$ を分数に直すと、$\dfrac{3}{10}$ です。分数の逆数は、分母と分子をひっくり返せば良いので、逆数は $\dfrac{10}{3}$ になります。

(6) $-0.29=-\dfrac{29}{100}$ の逆数は、$-\dfrac{100}{29}$
このように、マイナスの数の逆数は、マイナスの数になります。

なお、逆数の考え方は分数の割り算を計算するときに役に立ちます。

次回は 分数の計算の基本問題10問 を解説します。