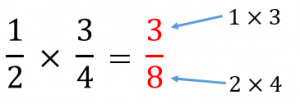
分数のかけ算は、分母どうし、分子どうしをそれぞれかけ算すればよい。
このページでは、分数と分数の掛け算について説明します。整数や帯分数が含まれる場合についての練習問題も解説します。3つの分数の掛け算のやり方も紹介します。
分数と分数の掛け算の練習問題
問題
以下を計算せよ:
(1) $\dfrac{1}{2}\times \dfrac{3}{4}$ (2) $\dfrac{5}{6}\times \dfrac{3}{10}$
答え
分母どうし、分子どうしをそれぞれかけ算する:
(1) $\dfrac{1}{2}\times\dfrac{3}{4}=\dfrac{1\times 3}{2\times 4}=$$\dfrac{3}{8}$
「$\dfrac{1}{2}$ を $4$ つに分けた $3$ 個ぶん」は、「$8$ 個に分けた $3$ 個ぶん」と確かに同じになっています。
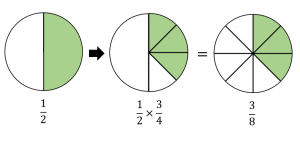
(2)
$\dfrac{5}{6}\times\dfrac{3}{10}\\=\dfrac{5\times 3}{6\times 10}\\
=\dfrac{1\times 1}{2\times 2}$
(分母分子をそれぞれ $5\times 3=15$ でわった)
$=$$\dfrac{1}{4}$
整数、帯分数が含まれる場合
問題
以下を計算せよ:
(3) $\dfrac{3}{8}\times 2$ (4) $2\dfrac{4}{7}\times \dfrac{5}{6}$
答え
(3) この場合、$2=\dfrac{2}{1}$ を使います:
$\dfrac{3}{8}\times 2=\dfrac{3}{8}\times\dfrac{2}{1}\\
=\dfrac{3\times 2}{8\times 1}$
$=$$\dfrac{3}{4}$
($2$ で約分した)
(4) 帯分数は仮分数の形に直します(→真分数、仮分数、帯分数の意味と例題):
$2\dfrac{4}{7}=\dfrac{2\times 7+4}{7}=\dfrac{18}{7}$
なので、
$2\dfrac{4}{7}\times \dfrac{5}{6}=\dfrac{18}{7}\times\dfrac{5}{6}\\
=\dfrac{18\times 5}{7\times 6}=\dfrac{3\times 5}{7\times 1}=\dfrac{15}{7}$
$=$$2\dfrac{1}{7}$
(最後に帯分数の形に戻した)
3つの分数のかけ算
問題
以下を計算せよ:
(5) $\dfrac{2}{3}\times\dfrac{5}{6}\times\dfrac{3}{10}$
答え
$\dfrac{2}{3}\times\dfrac{5}{6}\times\dfrac{3}{10}=\dfrac{2\times 5\times 3}{3\times 6\times 10}\\
=\dfrac{1\times 1\times 1}{1\times 3\times 2}$
$=$$\dfrac{1}{6}$
次回は 分数の割り算:やり方、整数や帯分数の場合 を解説します。
