ユニタリー行列、エルミート行列などの意味と関係

記号の意味、具体例

$I$ は単位行列です。→単位行列の定義といろいろな性質

$A^{\top}$ は $A$ の転置行列です。$A^{*}$ は随伴行列（共役転置行列）です。例えば $A=\begin{pmatrix}a&b\\c&d\end{pmatrix}$ に対して、$A^{\top}=\begin{pmatrix}a&c\\b&d\end{pmatrix}$、$A^{*}=\begin{pmatrix}\overline{a}&\overline{c}\\\overline{b}&\overline{d}\end{pmatrix}$ です。（$\overline{a}$ は $a$ の複素共役）

対称行列の例：$\begin{pmatrix}2&3\\3&1\end{pmatrix}$

エルミート行列の例：$\begin{pmatrix}2&4+i\\4-i&1\end{pmatrix}$

直交行列の例：$\begin{pmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{pmatrix}$

ユニタリー行列の例：$\begin{pmatrix}\frac{1}{\sqrt{2}}&\frac{i}{\sqrt{2}}\\\frac{i}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{pmatrix}$

行列の関係

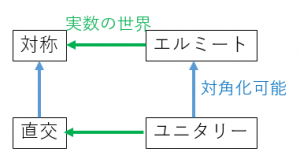
実行列では、$A^{\top}$ と $A^{*}$ は同じものなので、

・対称行列はエルミート行列でもある
・直交行列はユニタリー行列でもある

ことが分かります。また、

・対称行列は直交行列で対角化できる。
・エルミート行列はユニタリー行列で対角化できる。

ことが知られています。

その他の性質

・エルミート行列の対角成分は実数です。

・直交行列、ユニタリー行列の行ベクトルたちは、正規直交基底をなします。列ベクトルたちも正規直交基底をなします。→正規直交基底（定義、求め方、性質）

・対称行列、エルミート行列、直交行列、ユニタリー行列はいずれも $A^{*}A=AA^{*}$ を満たします。この式を満たす行列を正規行列と言います。紹介した4種類の行列はいずれも正規行列ですが、他にも正規行列は存在します。

次回は 固有値と固有ベクトルの求め方と計算ツール を解説します。