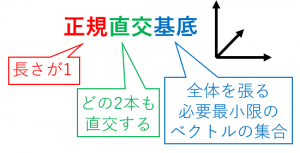
正規直交基底（定義、求め方、性質）

正規直交基底の例

例題

三本のベクトル：$\overrightarrow{v_1}=\begin{pmatrix}\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\\0\end{pmatrix}$、$\overrightarrow{v_2}=\begin{pmatrix}\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}\\0\end{pmatrix}$、$\overrightarrow{v_3}=\begin{pmatrix}0\\0\\1\end{pmatrix}$ が正規直交基底をなしていることを確認せよ。

解答

長さが１であることの確認
$|\overrightarrow{v_1}|=\sqrt{(\frac{1}{\sqrt{2}})^2+(\frac{1}{\sqrt{2}})^2}=1$
同様に、$|\overrightarrow{v_2}|=|\overrightarrow{v_3}|=1$ も簡単に確認できます。

互いに直交していることの確認
内積を計算すればOKです。
$\overrightarrow{v_1}\cdot\overrightarrow{v_2}\\
=\frac{1}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\cdot(-\frac{1}{\sqrt{2}})=0$
同様に、$\overrightarrow{v_1}\cdot\overrightarrow{v_3}=\overrightarrow{v_2}\cdot\overrightarrow{v_3}=0$ も簡単に確認できます。

基底であることの確認
三本のベクトルを並べた行列：
$(\overrightarrow{v_1}\:\overrightarrow{v_2}\:\overrightarrow{v_3})=\begin{pmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0\\0&0&1\end{pmatrix}$ が正則であることを確認すればOKです。

例えば、行列式を計算してみると、$-1$ となることから確認できます。

正規直交基底の作り方

（正規直交とは限らない）基底が与えられたときに、正規直交基底を求める方法（グラムシュミッドの直交化法）を紹介します。

長さを $1$ にするのは簡単（ベクトルを長さで割ればよいだけ）なので、どのように直交化するかがポイントです。

$\overrightarrow{v_1},\cdots,\overrightarrow{v_k}$ が正規直交かつ、$\overrightarrow{u}$ がそれらと一次独立のとき、
公式：$\overrightarrow{v}=\overrightarrow{u}-\displaystyle\sum_{i=1}^{k}(\overrightarrow{u}\cdot\overrightarrow{v}_i)\overrightarrow{v}_i$
という新しいベクトルは、$\overrightarrow{v_1},\cdots,\overrightarrow{v_k}$ たちと直交することを利用します！

例題

2本のベクトル：$\overrightarrow{u_1}=\begin{pmatrix}1\\1\end{pmatrix}$、$\overrightarrow{u_2}=\begin{pmatrix}1\\2\end{pmatrix}$、から正規直交基底 $\overrightarrow{v_1},\overrightarrow{v_2}$ を作れ。

解答

まず $\overrightarrow{u_1}$ を正規化して $\overrightarrow{v_1}$ を求める
$|\overrightarrow{u_1}|=\sqrt{2}$ より、$\overrightarrow{v_1}=\dfrac{\overrightarrow{u_1}}{\sqrt{2}}=\begin{pmatrix}\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{pmatrix}$
とすればよい。

次に、公式を使って $\overrightarrow{u_2}$ から $\overrightarrow{v_1}$ と直交するベクトル $\overrightarrow{v}$ を求める：
$\overrightarrow{v}=\overrightarrow{u_2}-(\overrightarrow{u_2}\cdot\overrightarrow{v_1})\overrightarrow{v_1}\\
=\begin{pmatrix}1\\2\end{pmatrix}-\dfrac{3}{\sqrt{2}}\begin{pmatrix}\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{pmatrix}\\=\begin{pmatrix}-\frac{1}{2}\\\frac{1}{2}\end{pmatrix}$

$\overrightarrow{v}$ を正規化して $\overrightarrow{v_2}$ を得る：
$\overrightarrow{v_2}=\dfrac{\overrightarrow{v}}{|\overrightarrow{v}|}=\begin{pmatrix}-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{pmatrix}$

三次元以上の場合も同様です。公式による直交化と正規化を交互に繰り返していき、$\overrightarrow{v_3},\overrightarrow{v_4},\cdots$ と順々に計算していくことになります。

直交行列の性質

正規直交基底をなすベクトルを並べた行列を直交行列と言います。

例えば、先ほどの例についての行列は、
$(\overrightarrow{v_1}\:\overrightarrow{v_2}\:\overrightarrow{v_3})=\begin{pmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0\\0&0&1\end{pmatrix}$
です。

直交行列の行列式は必ず $\pm 1$ になる、という性質があります。

次回は 動径基底関数（RBF）に関連する知識の整理 を解説します。