最終更新日 2019/05/12
円柱の体積 $V$ は、
円周率×半径×半径×高さ
円柱の表面積 $S$ は
$2$×円周率×半径×半径
+$2$×円周率×半径×高さ

このページでは、円柱の表面積について詳しく説明します。体積の求め方の詳細は三角柱、四角柱、円柱の体積の求め方に書いています。
円柱の表面積の求め方
円柱の表面積は
・底面の面積
・天面の面積
・側面の面積
の和です。

底面
は半径 $r$ の円なので、面積は $\pi r^2$ です。
関連:円の面積を積分で計算する2通りの方法
天面
も底面と同じく、面積は $\pi r^2$ です。
側面
は長方形です。縦の長さは $h$ です。横の長さは(底面の円周の長さと同じなので)$2\pi r$ です。よって、側面積は $2\pi rh$ です。
よって、表面積は、3つを足すと、
$\pi r^2+\pi r^2+2\pi rh\\
=2\pi r^2+2\pi rh$
となります。
例題
図のような円柱の表面積を求めよ。(底面の半径は $3\:\mathrm{cm}$、円柱の高さは $4\:\mathrm{cm}$)
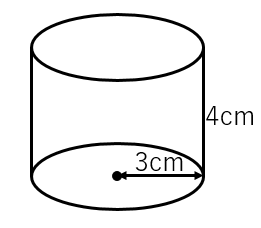
底面の面積は、
$\pi \times 3^2=9\pi$
天面の面積は、同じく $9\pi$
側面の面積は、
$(2\pi\times 3)\times 4=24\pi$
よって、表面積は、
$9\pi+9\pi+24\pi=42\pi$
特に、円周率を $3.14$ とすると、
$131.88$
となります。
円柱の表面積計算ツール
次回は 立方体と直方体の見取り図の書き方 を解説します。
