半径 $r$ の円の面積は $\pi r^2$ である。
これを積分を使って証明してみましょう。
(前半)積分の式を作る
まず、$xy$ 座標平面で考えてみます。半径 $r$ の円の方程式は $x^2+y^2=r^2$ です。これを $y$ について解くと $y=\pm\sqrt{r^2-x^2}$ となります。
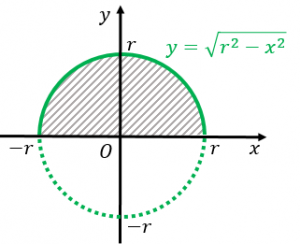
上側半分を表す式は、プラスの方を採用して $y=\sqrt{r^2-x^2}$ となります。
よって、円の面積 $S$ の半分は、
$\dfrac{S}{2}=\displaystyle\int_{-r}^r\sqrt{r^2-x^2}dx$
となります。
(後半)積分を計算する
この定積分の計算には置換積分を使います。$x=r\sin\theta\:(-\frac{\pi}{2}\leq \theta \leq \frac{\pi}{2})$ と置換すると、$\dfrac{dx}{d\theta}=r\cos\theta$ より、
$\dfrac{S}{2}=\displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sqrt{r^2-r^2\sin^2\theta}\cdot(r\cos\theta)d\theta\\
=r^2\displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^2\theta d\theta$
$\cos^2\theta$ の積分には半角の公式を使います。
関連:sin^2x、cos^2x、tan^2xの積分
$\dfrac{S}{2}=r^2\displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\dfrac{1+\cos 2\theta}{2}d\theta\\
=\dfrac{r^2}{2}\left[\theta+\dfrac{\sin 2\theta}{2}\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\\
=\dfrac{\pi r^2}{2}$
よって、円の面積は $S=\pi r^2$ となります。
別解:極座標で計算する方法
高校数学の範囲外ですが、極座標で計算することもできます。
半径 $r$ の円の面積は、
$S=\displaystyle\int_{x^2+y^2\leq r^2}1dxdy$
(重積分による面積の定義)
これを極座標に変数変換すると、ヤコビアンは $R$ なので、
$S=\displaystyle\int_{0}^{r}dR\displaystyle\int_{0}^{2\pi}Rd\theta$
となります。
$\theta\to R$ の順に積分すると,
$S=2\pi\displaystyle\int_{0}^{r}RdR\\
=2\pi\dfrac{r^2}{2}$
$=\pi r^2$
となります。
次回は 楕円に関する公式まとめ を解説します。
