三角柱の体積、四角柱の体積、円柱の体積
は全て底面積×高さで計算できる。
「柱」と名のつく立体の体積は、全て底面積×高さで求めることができます!
三角柱の体積
例題1:図のような三角柱の体積を求めよ。(底面は直角三角形、$2\:\mathrm{cm}$ と $5\:\mathrm{cm}$ の辺の間が直角。高さは $4\:\mathrm{cm}$)

底面積さえ計算してしまえば「柱」の体積を計算できます。
この場合、底面は直角三角形なので、その面積は、
$2\times 5\div 2=5\:\mathrm{cm}^2$ です。
体積を求めるには、これに高さをかければよいので、
$5\times 4=20\:\mathrm{cm}^3$
が答えとなります。
四角柱の体積
例題2:図のような四角柱の体積を求めよ。(底面は台形、上底が $2\:\mathrm{cm}$、下底が $6\:\mathrm{cm}$、台形の高さは $3\:\mathrm{cm}$、四角柱の高さは $4\:\mathrm{cm}$)

この場合、底面は台形なので、その面積は、
$(2+6)\times 3\div 2=12\:\mathrm{cm}^2$
です。
体積を求めるには、これに高さをかければよいので、
$12\times 4=48\:\mathrm{cm}^3$
が答えとなります。
関連:台形の面積を求める公式
円柱の体積
例題3:図のような円柱の体積を求めよ。(底面の半径は $3\:\mathrm{cm}$ 円柱の高さは $4\:\mathrm{cm}$)
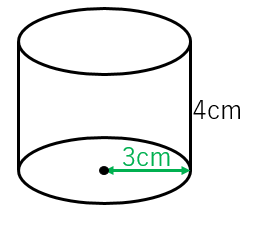
底面は円なので、円周率を $\pi$ とすると、その面積は、
$3\times 3\times \pi=9\pi\:\mathrm{cm}^2$
です。
体積を求めるには、これに高さをかければよいので、
$9\pi\times 4=36\pi\:\mathrm{cm}^3$
が答えとなります。
次回は 三角錐、四角錐、円錐の体積を求める公式と例題 を解説します。
