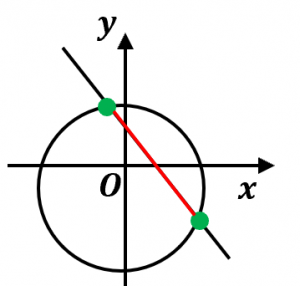
座標平面上における円と直線について
・円と直線の共有点の個数は?
・共有点の座標の計算方法は?
・円が直線から切り取る線分の長さは?
といった疑問にお答えします。
円と直線の共有点の個数
連立方程式
$\begin{eqnarray}\begin{cases}x^2+y^2=4\\y=2x-3\end{cases}\end{eqnarray}$
の解が円と直線の交点の座標です。
下の式を上の式に代入すると、
$x^2+\left(2x-3\right)^2=4$
$x^2+4x^2-12x+9=4$
$5x^2-12x+5=0$
この二次方程式の解の個数は、判別式 $D$ の符号から分かります。
$\dfrac{D}{4}=(-6)^2-5\cdot 5=11 > 0$
より、二次方程式の解は2つです。
よって、円と直線は($x$ 座標が異なる)2つの点で交わることが分かります。つまり、答えは2つです。
このように、連立方程式を最後まで解かなくても、判別式の符号を見るだけで、円と直線の共有点の個数が分かります。
円と直線の共有点の座標
共有点の個数だけなら判別式の符号から分かりましたが、共有点の座標を求める場合には二次方程式を解く必要があります。
円と直線の方程式は、最初の例題と同じです。よって、さきほどと同じ二次方程式
$5x^2-12x+5=0$
をbが偶数の場合の解の公式を使って解くと、
$x=\dfrac{6\pm\sqrt{(-6)^2-5\cdot 5}}{5}\\
=\dfrac{6\pm\sqrt{11}}{5}$
$x=\dfrac{6+\sqrt{11}}{5}$ のとき、
$y=2x-3\\
=\dfrac{-3+2\sqrt{11}}{5}$
$x=\dfrac{6-\sqrt{11}}{5}$ のときも同様に計算すると、$y=\dfrac{-3-2\sqrt{11}}{5}$
よって、答えは
$\left(\dfrac{6+\sqrt{11}}{5},\dfrac{-3+2\sqrt{11}}{5}\right)$ と $\left(\dfrac{6-\sqrt{11}}{5},\dfrac{-3-2\sqrt{11}}{5}\right)$
最初の例題に比べて計算が複雑になりました。
円が直線から切り取る線分の長さ
円と直線の式は、今までの例題と同じものです。
円と直線の交点の座標を計算してから、二点間の距離を求める公式を使ってもよいのですが、解と係数の関係を使えば計算が少し楽になります。
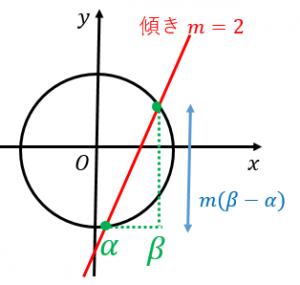
図における $\alpha$、$\beta$ は
$5x^2-12x+5=0$
の解なので、解と係数の関係より
$(\alpha-\beta)^2=(\alpha+\beta)^2-4\alpha\beta\\
=\dfrac{12^2}{5^2}-4\cdot 1\\
=\dfrac{44}{25}$
よって、$\beta-\alpha=\dfrac{2\sqrt{11}}{5}$
よって、線分の長さは三平方の定理より
$\sqrt{(\beta-\alpha)^2+\{m(\beta-\alpha)\}^2}\\
=\sqrt{1+m^2}(\beta-\alpha)\\
=\sqrt{5}\cdot\dfrac{2\sqrt{11}}{5}$
$=\dfrac{2\sqrt{55}}{5}$
次回は 2つの円の交点の座標を求める+答えの確認方法 を解説します。
