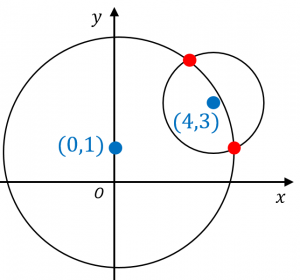
2つの円の交点(共有点)の座標は、連立方程式を解くことで求めることができます。
交点の座標の求め方
円1:$x^2+(y-1)^2=25$
円2:$(x-4)^2+(y-3)^2=5$
の交点の座標を求めよ。
解答
まず、2つの円の式をそれぞれ展開します:
$x^2+y^2-2y+1=25$
$x^2-8x+16+y^2-6y+9=5$
上の式から下の式を引くと、
$8x-16+4y-8=20$
つまり、
$8x+4y=44$
$2x+y=11$
$y=11-2x$
これを、円1の式に代入すると、
$x^2+(10-2x)^2=25$
次に、この二次方程式を解きます:
$x^2+100-40x+4x^2=25$
$5x^2-40x+75=0$
$x^2-8x+15$
$(x-3)(x-5)=0$
$x=3,5$
これを緑の式に代入すると、$y$ はそれぞれ
$5$ と $1$ になります。
よって、交点の座標は、$(3,5)$ と $(5,1)$ になります。
検算方法
答えが正しいかどうかを確認する方法を2つ紹介します。
方法1.オンラインのツールを使う
wolframalpha.com にアクセスし、
solve (x-1)^2+y^2=25,(x-3)^2+(y-4)^2=5
のように入力すれば、答えが確認できます。
ついでに座標平面上のグラフも確認できます。
方法2.もとの円の式に答えを代入して確認する
例えば、$x=3$、$y=5$ をもとの円の式:
$x^2+(y-1)^2=25$
に代入すると、
$3^2+(5-1)^2=25$
つまり、$9+16=25$ となり、確かに成立しています。
共有点の個数
2つの円の交点(共有点)の個数について、
1.共有点を2つ持つ
2.共有点を1つ持つ(接する)
3.共有点を持たない
の3つのパターンがあります。
1の場合には、連立方程式の解が2ペアでてきます。
2の場合には、連立方程式の解が1ペアでてきます。
3の場合には、連立方程式から実数解は得られません。
交点を通る直線
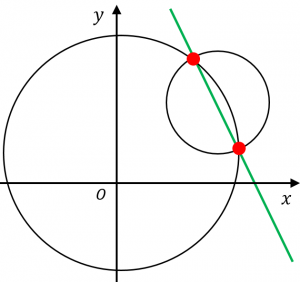
例えば、先ほどの例題では、円の交点を通る直線の方程式は、
$y=11-2x$
です。
次回は 二次関数のx軸、y軸、原点に関する対称移動 を解説します。
