二点間の距離を求める公式（2次元、3次元）

このページでは、
・公式の証明方法は？
・３次元の場合の距離公式はどうなるのか？
といった、二点間の距離公式についての疑問にお答えします。

平面上における二点間の距離公式

一般的な二点間の距離公式：
$(x_1,y_1)$ と $(x_2,y_2)$ を結ぶ線分の長さは、
$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
になります。

二点間の距離公式より、距離は、
$d=\sqrt{(3-(-2))^2+(4-0)^2}\\
=\sqrt{25+16}\\
=\sqrt{41}$
となります。

距離公式の証明

二次元座標平面上の2点 $A(x_1,y_1)$ と $B(x_2,y_2)$ の距離を計算してみましょう。

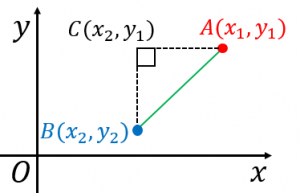
図のように点 $C$ を置いて、直角三角形 $ABC$ を作ってみます。
$AC$ の長さは $|x_1-x_2|$ となります。
（図では $x_1 > x_2$ なので $AC$ の長さは $x_1-x_2$ ですが、$x_1 < x_2$ の場合も一緒に扱うためには絶対値が必要です。）

また、同様に $BC$ の長さは $|y_1-y_2|$ となります。

よって、三平方の定理を使うと
$AB=\sqrt{AC^2+BC^2}\\
=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
となります。

3次元空間における二点間の距離公式

一般的な二点間の距離公式：
$(x_1,y_1,z_1)$ と $(x_2,y_2,z_2)$ を結ぶ線分の長さは、
$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

公式より、二点間の距離は、
$d=\sqrt{(1-3)^2+(0-4)^2+(-2-5)^2}\\
=\sqrt{4+16+49}\\
=\sqrt{69}$
になります。

公式の証明：
三次元座標空間上の2点 $A(x_1,y_1,z_1)$ と $B(x_2,y_2,z_2)$ の距離を計算してみましょう。
各辺が座標軸に平行な直方体で、$A,B$ が頂点（のうちの2つ）になるようなものを作ってみます。

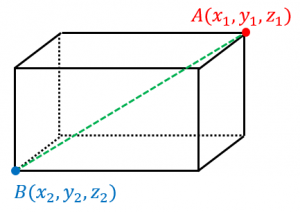
平面の場合と同じ考え方により、3つの異なる方向の辺の長さはそれぞれ
$|x_1-x_2|,|y_2-y_2|,|z_1-z_2|$
となります。

よって、直方体の対角線の長さを求める公式により、
$AB\\
=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$
となります。

片方が原点の場合

二次元平面の場合：
$(x,y)$ から原点までの距離は、
$\sqrt{x^2+y^2}$

三次元空間の場合：
$(x,y,z)$ から原点までの距離は、
$\sqrt{x^2+y^2+z^2}$

次回は 座標平面上で三角形の面積を計算する公式 を解説します。