遠心力について詳しく解説します。
遠心力の意味や、遠心力を計算するための3つの公式と、その証明を紹介します。
遠心力とは
遠心力の例:
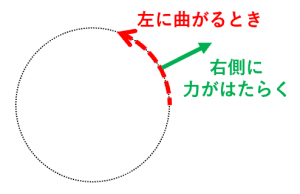
車に乗っていて左に曲がるとき、右側に引っ張られる(円の中心から離れる)ような力を感じると思います。これが遠心力です。
遠心力は速さの二乗に比例する
例えば、同じカーブを曲がるとき、
・速さが2倍だと4倍の遠心力がかかる
・速さが3倍だと9倍の遠心力がかかる
と言えます。
そのため、カーブを曲がるときは十分に減速しておかないと、大きな遠心力を受けるので危ない!と言えます。
実際、$v$ を速さ、$r$ を円運動の半径とすると、遠心力の大きさは
$F=m\dfrac{v^2}{r}$
で計算されます(最後に証明します)。遠心力の大きさは速さ $v$ の二乗に比例することが分かります。
遠心力を計算する公式
遠心力の大きさを計算する公式は、さきほど説明した
【速さと半径が分かっている場合】
$F=m\dfrac{v^2}{r}$
の他にも
【半径と角速度が分かっている場合】
$F=mr\omega^2$
【速さと角速度が分かっている場合】
$F=mv\omega$
があります。$\omega$ は角速度(1秒あたり何ラジアン進むか)です。
3つの公式は覚えなくてもよい
実際、$v=r\omega$ という公式(→補足)を
$F=m\dfrac{v^2}{r}$
に代入すれば
$F=mr\omega^2$
という公式をすぐに導出することができます。また、$r$ を消去すれば
$F=mv\omega$
を導出することができます。
補足:
$v=r\omega$ は重要な公式なので知らなかった人はぜひ覚えておきましょう。実際、
おうぎ形の弧の長さ=半径×中心角
(おうぎ形の弧長、面積、中心角、半径)
なので、
1秒間に進む弧の長さ=半径×1秒間に進む中心角
つまり、
$v=r\omega$
が成立します。
遠心力の公式の証明
ちなみに、残りの2つは $v=r\omega$ を使えば導出できます。
きちんと証明を理解するためには、微分が必要です。
証明:
加速度 $\overrightarrow{a}$ で運動する物体には、$-m\overrightarrow{a}$ の慣性力が働きます。これが遠心力です。
あとは、円運動の加速度 $\overrightarrow{a}$ を計算します。
まず、円運動の中心を原点とする座標平面で考えると、半径 $r$ の円運動をしている物体の時刻 $t$ における位置は
$(r\cos\omega t,r\sin\omega t)$
と表すことができます。
速度は位置を時刻で微分したものなので、
$\overrightarrow{v}=(-r\omega \sin\omega t,r\omega \cos\omega t)$
となります。
さらに、加速度は速度の微分なので、
$\overrightarrow{a}=(-r\omega^2 \cos\omega t,-r\omega^2\sin\omega t)$
よって、遠心力は
$-m\overrightarrow{a}=(mr\omega^2\cos\omega t,mr\omega^2\sin\omega t)$
となります。
つまり、
・遠心力の向きは円の外側に向かう
・遠心力の大きさは $mr\omega^2$
であることが分かります。
次回は 1ニュートンは何キログラム重なのか解説 を解説します。
