真分数、仮分数、帯分数の意味と例題

具体例

真分数の例：$\dfrac{2}{3}$、$\dfrac{5}{6}$、$\dfrac{2}{4}$
→分子が分母より小さい

仮分数の例：$\dfrac{3}{2}$、$\dfrac{4}{4}$、$\dfrac{20}{8}$
→分子が分母より大きいまたは等しい

帯分数の例：$1\tfrac{2}{3}$（$1$ と $\tfrac{2}{3}$ と読む。$1+\tfrac{2}{3}$のこと）、$3\tfrac{1}{4}$
→整数と真分数のたし算

仮分数を帯分数に直す

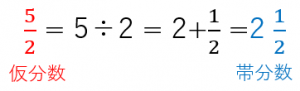
問題

次の仮分数を帯分数、または整数で表わせ。
(1) $\dfrac{5}{2}$　　(2) $\dfrac{37}{17}$　　(3) $\dfrac{15}{5}$

答え

(1) $\dfrac{5}{2}$ は $5\div 2$ のこと。実際に$5\div 2$ というわり算をやってみると、商は $2$ で余りは $1$ となる。つまり、$5=2\times 2+1$ となる。
よって、$\dfrac{5}{2}=\dfrac{2\times 2+1}{2}=2+\dfrac{1}{2}$$=2\dfrac{1}{2}$
（これは帯分数！）

(2) 数字が大きくなっても同じ。$37\div 17$ というわり算をやってみると、商は $2$ で余りは $3$ となる。つまり、$37=17\times 2+3$ となる。
よって、$\dfrac{37}{17}=\dfrac{17\times 2+3}{17}=2+\dfrac{3}{17}$$=2\dfrac{3}{17}$
（これは帯分数！）

(3) $15\div 5$ というわり算をやってみると、商は $3$ で余りは $0$ となる。
よって、$\dfrac{15}{5}=3$
（これは整数！）

関連：分数の計算の基本問題10問

帯分数を仮分数に直す

問題

次の帯分数を仮分数で表わせ。
(1) $1\dfrac{2}{5}$　　(2) $5\dfrac{3}{8}$

答え

(1) $1\dfrac{2}{5}=1+\dfrac{2}{5}=\dfrac{5}{5}+\dfrac{2}{5}=\dfrac{7}{5}$

(2) $5\dfrac{3}{8}=5+\dfrac{3}{8}=\dfrac{5\times 8}{8}+\dfrac{3}{8}=\dfrac{43}{8}$

次回は 分数の足し算、引き算 を解説します。