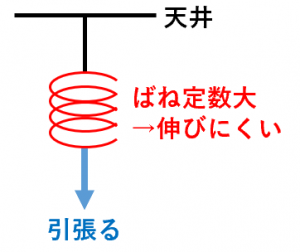
ばね定数とは「ばねの伸びにくさ」を表す値です。ばね定数が大きいほど「硬いばね」と言うことができます。
ばね定数の意味や計算方法、およびばね定数の合成(直列・並列の場合)について分かりやすく解説します。
ばね定数の定義
ばねに加える力を $F$、ばねの伸びを $x$ とすると($F$ が小さいときには)$F$ は $x$ に比例します。
つまり、$F=kx$ という関係式が成立します。この定数 $k$ のことをばね定数と言います。
例えば、ばねに $30\:\mathrm{N}$ の力を加えたときに $0.02\:\mathrm{m}$ 伸びるとき、ばね定数は、
$30\div 0.02=1500\:\mathrm{N/m}$
となります。
ばね定数の単位
$1\:\mathrm{N/m}$ は「約 $100$ グラムのおもりによって $1$ メートル伸びる」ほどの強さです。
$1\:\mathrm{N/mm}$ は「約 $100$ グラムのおもりによって $1$ ミリメートル伸びる」ほどの強さです。「約 $1$ キログラムのおもりによって $1$ センチメートル伸びる」と言うこともできます。
ばね定数の合成
例えば、$k_1=10\:\mathrm{N/mm}$、$k_2=20\:\mathrm{N/mm}$ のとき、全体のばね定数は $30\:\mathrm{N/mm}$ になります。
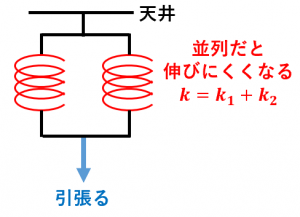
このように、並列につなぐと、ばね定数は大きくなります。つまり、1本のときよりも、2本並列につないだときの方が、ばねは伸びにくくなります。
$\dfrac{1}{k}=\dfrac{1}{k_1}+\dfrac{1}{k_2}$ と書くこともできます。
例えば、$k_1=10\:\mathrm{N/mm}$、$k_2=20\:\mathrm{N/mm}$ のとき、全体のばね定数は $\dfrac{1}{\frac{1}{10}+\frac{1}{20}}=\dfrac{20}{3}\fallingdotseq 6.7\:\mathrm{N/mm}$ になります。
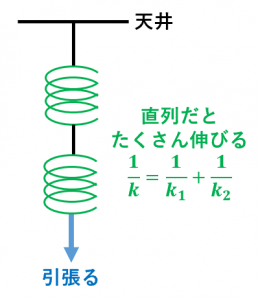
このように、直列につなぐと、ばね定数は小さくなります。つまり、1本のときよりも、2本直列につないだときの方が、ばねは伸びやすくなります。
※オームの法則を使って合成抵抗を計算する場合の公式は、
直列の場合が $R=R_1+R_2$
並列の場合が $\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}$
でした。直列と並列がちょうど逆になっているので注意が必要です。
参考:合成抵抗の計算方法とツール(直列接続、並列接続)
次回は mmHgをPaやatmに変換する方法とツール を解説します。
