直列接続の合成抵抗の公式:
$R=R_1+R_2$
並列接続の合成抵抗の公式:
$\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}$
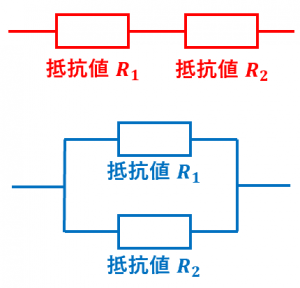
合成抵抗を計算する公式を、直列の場合と並列の場合それぞれ解説します。3個以上の抵抗の合成についても説明し、最後に合成抵抗の計算ツールを紹介します。
直列接続の合成抵抗
$R=R_1+R_2$
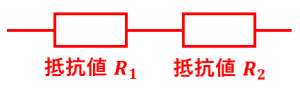
例えば、$10\Omega$ の抵抗と $20\Omega$ の抵抗を直列に接続した場合、回路全体の合成抵抗は、
$10+20=30\Omega$
になります。
直列接続の合成抵抗が足し算になる理由
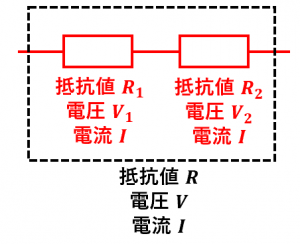
キルヒホッフの法則より、
$V=RI$
$V_1=R_1I$
$V_2=R_2I$
となります。さらに、直列接続なので、
$V=V_1+V_2$
が成立します。よって、
$RI=R_1I+R_2I$
両辺を $I$ で割ると、
$R=R_1+R_2$
となります。
並列接続の合成抵抗
$\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}$
という公式で計算することができます:
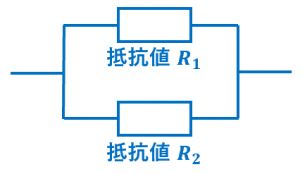
例えば、$10\Omega$ の抵抗と $30\Omega$ の抵抗を並列に接続した場合、回路全体の合成抵抗を $R$ とすると、
$\dfrac{1}{R}=\dfrac{1}{10}+\dfrac{1}{30}\\
=\dfrac{2}{15}$
となります。つまり、
$R=\dfrac{15}{2}=7.5\Omega$
になります。
並列接続の合成抵抗の公式の理由
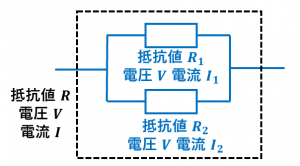
キルヒホッフの法則より、
$V=RI$
$V=R_1I_1$
$V=R_2I_1$
となります。さらに、並列接続なので、
$I=I_1+I_2$
が成立します。よって、
$\dfrac{V}{R}=\dfrac{V}{R_1}+\dfrac{V}{R_2}$
となります。両辺を $V$ で割ると、
$\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}$
となります。
抵抗値が3つ以上の場合
抵抗値が $R_1,\dots,R_n$ である $n$ 個の抵抗を、全て直列につないだ場合の合成抵抗 $R$ は、
$R=R_1+R_2+\dots +R_n$
になります。
同様に全て並列につないだ場合の合成抵抗 $R$ は、
$\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dots +\dfrac{1}{R_n}$
で計算できます。
3個以上の場合の公式も、抵抗が2個の場合と同様に、キルヒホッフの法則を使って証明することができます。
合成抵抗の計算ツール
次回は 消費電力(ワット)を計算する3つの方法(電流、電圧、抵抗から) を解説します。
