比例定数の意味と求め方

比例定数とは

例えば、$x$ と $y$ の間に、$y=2x$ という比例関係が成り立つとき、
比例定数は $2$ です。

同様に、
$y=-3x$ なら比例定数は $-3$
$y=0.123x$ なら比例定数は $0.123$
になります。

※比例については、比例（数学）の意味を分かりやすく解説をご覧ください。

グラフの傾き

比例のグラフは、原点を通る直線になります。この直線の傾きが比例定数になります。

例えば、$y=2x$ のグラフは図のようになりますが、
傾きは、$2$ になっています。
つまり、比例定数は $2$ です。

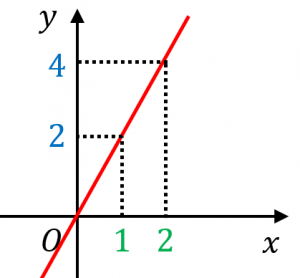
※傾きとは、$x$ が $1$ 増加したときに、$y$ がどれくらい増加するかを表す量です。この例では、$x$ が $1$ 増加すると、$y$ が $2$ 増加するので、傾きは $2$ です。

比例定数を求める例題

$y=ax$ の両辺を $x$ で割ると、$a=\dfrac{y}{x}$ になります。
つまり、$y$ の値を $x$ の値で割れば、比例定数 $a$ を求めることができます。

この例題では、比例定数は、
$6\div 3=2$
になります。

余談

・反比例 $y=\dfrac{a}{x}$ に対しても、$a$ のことを比例定数と呼ぶことがあります。$y=a\times\dfrac{1}{x}$ と書けば、$y$ は $\dfrac{1}{x}$ に比例する、とみなすことができるからです。

・一般の一次関数 $y=ax+b$ に対して、$a$ のことは比例定数とは言いません。
関連：傾きと切片の意味と求め方を丁寧に解説

次回は 一次関数について基本から分かりやすく解説 を解説します。