単位円を用いた三角比の定義:
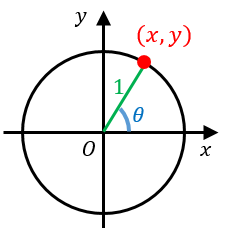
1. 単位円(中心が原点で半径 $1$ の円)を書く
2. 「$x$ 軸の正の部分」を $\theta$ だけ反時計周りに回転させた線と単位円の交点の座標を $(x,y)$ とおく
3. $\sin\theta=y$、$\cos\theta=x$、$\tan\theta=\dfrac{y}{x}$
有名角の三角比の表
$0^{\circ}\leq\theta\leq 90^{\circ}$ の場合の有名角の表です:
$\begin{array}{|c|c|c|c|c|c|}\hline \theta&0^{\circ}&30^{\circ}&45^{\circ}&60^{\circ}&90^{\circ}\\
\hline\sin\theta &0&\dfrac{1}{2}&\dfrac{1}{\sqrt{2}}&\dfrac{\sqrt{3}}{2}&1\\
\hline\cos\theta &1&\dfrac{\sqrt{3}}{2}&\dfrac{1}{\sqrt{2}}&\dfrac{1}{2}&0\\
\hline\tan\theta &0&\dfrac{1}{\sqrt{3}}&1&\sqrt{3}&\infty\\\hline\end{array}$
鈍角の場合の有名角の表です:
$\begin{array}{|c|c|c|c|c|}\hline \theta&120^{\circ}&135^{\circ}&150^{\circ}&180^{\circ}\\
\hline\sin\theta &\dfrac{\sqrt{3}}{2}&\dfrac{1}{\sqrt{2}}&\dfrac{1}{2}&0\\
\hline\cos\theta &-\dfrac{1}{2}&-\dfrac{1}{\sqrt{2}}&-\dfrac{\sqrt{3}}{2}&-1\\
\hline\tan\theta &-\sqrt{3}&-1&-\dfrac{1}{\sqrt{3}}&0\\\hline\end{array}$
この表の値を1つずつ図で確認してみましょう。
$0^{\circ}$ の三角比
この記事で登場する円は全て半径 $1$ です。
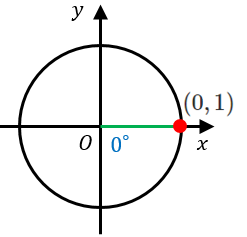
$y$ 座標は $0$ なので、$\sin 0^{\circ}=0$
$x$ 座標は $1$ なので、$\cos 0^{\circ}=1$
傾きは $\dfrac{y}{x}=0$ なので、$\tan 0^{\circ}=0$
$30^{\circ}$ の三角比
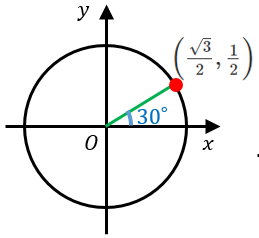
$y$ 座標は $\dfrac{1}{2}$ なので、$\sin 30^{\circ}=\dfrac{1}{2}$
$x$ 座標は $\dfrac{\sqrt{3}}{2}$ なので、$\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$
傾きは $\dfrac{y}{x}=\dfrac{1}{\sqrt{3}}$ なので、$\tan 30^{\circ}=\dfrac{1}{\sqrt{3}}$
注:$30^{\circ}$、$60^{\circ}$、$90^{\circ}$ の直角三角形の辺の比が $1:2:\sqrt{3}$ であることを使っています。
関連:「30°、60°、90°」と「45°、45°、90°」の直角三角形の辺の比
$45^{\circ}$ の三角比
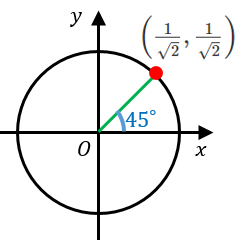
$y$ 座標は $\dfrac{1}{\sqrt{2}}$ なので、$\sin 45^{\circ}=\dfrac{1}{\sqrt{2}}$
$x$ 座標は $\dfrac{1}{\sqrt{2}}$ なので、$\cos 45^{\circ}=\dfrac{1}{\sqrt{2}}$
傾きは $\dfrac{y}{x}=1$ なので、$\tan 45^{\circ}=1$
注:$45^{\circ}$、$45^{\circ}$、$90^{\circ}$ の直角三角形の辺の比が $1:1:\sqrt{2}$ であることを使っています。
関連:直角二等辺三角形の辺の長さの求め方
$60^{\circ}$ の三角比
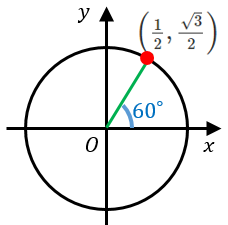
$y$ 座標は $\dfrac{\sqrt{3}}{2}$ なので、$\sin 60^{\circ}=\dfrac{\sqrt{3}}{2}$
$x$ 座標は $\dfrac{1}{2}$ なので、$\cos 60^{\circ}=\dfrac{1}{2}$
傾きは $\dfrac{y}{x}=\sqrt{3}$ なので、$\tan 60^{\circ}=\sqrt{3}$
$90^{\circ}$ の三角比
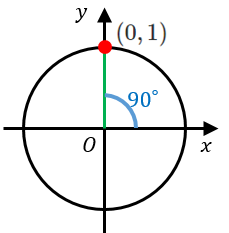
$y$ 座標は $1$ なので、$\sin 90^{\circ}=1$
$x$ 座標は $0$ なので、$\cos 90^{\circ}=0$
傾きは定義できないので、$\tan 90^{\circ}$ は定義できません。
$120^{\circ}$ の三角比
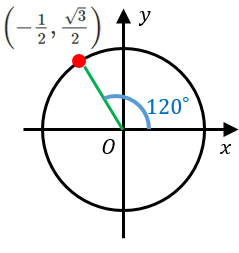
$y$ 座標は $\dfrac{\sqrt{3}}{2}$ なので、$\sin 120^{\circ}=\dfrac{\sqrt{3}}{2}$
$x$ 座標は $-\dfrac{1}{2}$ なので、$\cos 120^{\circ}=-\dfrac{1}{2}$
傾きは $\dfrac{y}{x}=-\sqrt{3}$ なので、$\tan 120^{\circ}=-\sqrt{3}$
直角でも鈍角でも、考え方は同じです。
$135^{\circ}$ の三角比
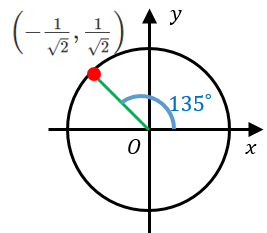
$y$ 座標は $\dfrac{1}{\sqrt{2}}$ なので、$\sin 135^{\circ}=\dfrac{1}{\sqrt{2}}$
$x$ 座標は $-\dfrac{1}{\sqrt{2}}$ なので、$\cos 135^{\circ}=-\dfrac{1}{\sqrt{2}}$
傾きは $\dfrac{y}{x}=-1$ なので、$\tan 135^{\circ}=-1$
$150^{\circ}$ の三角比
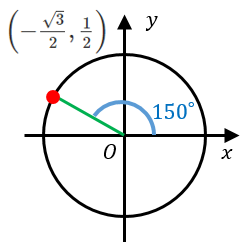
$y$ 座標は $\dfrac{1}{2}$ なので、$\sin 150^{\circ}=\dfrac{1}{2}$
$x$ 座標は $-\dfrac{\sqrt{3}}{2}$ なので、$\cos 150^{\circ}=-\dfrac{\sqrt{3}}{2}$
傾きは $\dfrac{y}{x}=-\dfrac{1}{\sqrt{3}}$ なので、$\tan 150^{\circ}=-\dfrac{1}{\sqrt{3}}$
$180^{\circ}$ の三角比
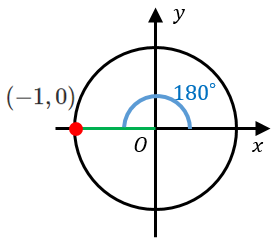
$y$ 座標は $0$ なので、$\sin 180^{\circ}=0$
$x$ 座標は $-1$ なので、$\cos 180^{\circ}=-1$
傾きは $\dfrac{y}{x}=0$ なので、$\tan 180^{\circ}=0$
次回は 三角関数の加法定理に関する公式全22個(導出の流れつき) を解説します。
