
「30°、60°、90°」の直角三角形の3辺の比は $1:2:\sqrt{3}$
「45°、45°、90°」の直角三角形の3辺の比は $1:1:\sqrt{2}$
「30°、60°、90°」の直角三角形
「30°、60°、90°」の直角三角形の辺の比について考えてみましょう。
実は、この直角三角形は正三角形 $ABC$ の半分になっています。理由は「正三角形の頂角の二等分線は底辺の垂直二等分線と一致する」からです。
関連:二等辺三角形の4つの性質と4つの条件
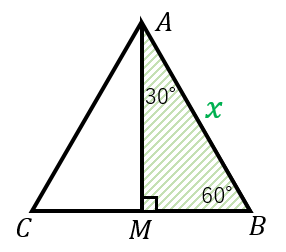
$AB=x$ として、$BM$、$AM$ の長さを計算してみましょう。$M$ は $BC$ の中点なので $BM=\dfrac{1}{2}BC=\dfrac{1}{2}x$ となります。
また、三平方の定理より、
$AM^2=AB^2-BM^2\\
=x^2-\left(\dfrac{x}{2}\right)^2\\
=\dfrac{3}{4}x^2$
→ $AM=\dfrac{\sqrt{3}}{2}x$
よって、3辺の長さの比は
$BM:AB:AM=\dfrac{1}{2}x:x:\dfrac{\sqrt{3}}{2}x$
$=1:2:\sqrt{3}$
となります。
「45°、45°、90°」の直角三角形
こちらは2つの角が等しいので、二等辺三角形になります。つまり、直角二等辺三角形です。
$BC=x$ とすると、二等辺三角形なので $AC=x$ となります。
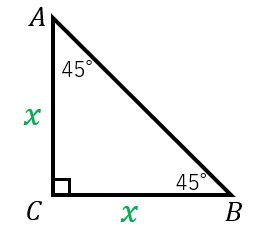
三平方の定理より、
$AB^2=x^2+x^2=2x^2$
→ $AB=\sqrt{2}x$
よって、3辺の長さの比は、
$BC:AC:AB=1:1:\sqrt{2}$
となります。
補足、まめ知識
・「45°、45°、90°」の直角三角形の辺の長さの比を「$\sqrt{2}:1:1$」や「$1:\sqrt{2}:1$」と言うこともできますが「$1:1:\sqrt{2}$」という順番で覚えている人が多いと思います。
・同様に「30°、60°、90°」の直角三角形の辺の比も「$1:2:\sqrt{3}$」で覚えている人が多いです。
・この2種類の直角三角形は三角定規にもなっていて非常に有名です。「30°を含む直角三角形」「45°を含む直角三角形」などと言われることもあります。
・この2種類以外にも「15°、75°、90°」の直角三角形の辺の比も頑張れば計算することができます:
sin15度、cos15度、tan15度の値と求め方
次回は 正三角形の内接円の半径と外接円の半径 を解説します。
