y=(logx)^2の微分、積分、グラフ

微分

まずは簡単な微分からです。実は、これは積分の準備にもなっています！

～やり方その１～
合成関数の微分公式を使うと、
$(\log x)^2$ の微分は、
$2(\log x)(\log x)’$
となります。

$\log x$ の微分は $\dfrac{1}{x}$ なので、結局
$\dfrac{2\log x}{x}$ となります。

～やり方その２～
$(\log x)^2=(\log x)(\log x)$ の微分は、積の微分公式より、
$(\log x)(\log x)’+(\log x)'(\log x)\\
=\dfrac{2\log x}{x}$

不定積分

logの二乗の積分です。logx、xlogx、logx/x、1/xlogxの積分にもあるように、$\log$ が絡む積分は部分積分を使うことが多いです。
部分積分について、基本的な使い方やコツを分かりやすく解説

$\displaystyle\int(\log x)^2dx\\
=\displaystyle\int 1\cdot(\log x)^2dx$ と見て部分積分を使いますが、先ほど見たように $(\log x)^2$ の微分は $\dfrac{2\log x}{x}$ なので、上式は、
$x(\log x)^2-\displaystyle\int x\cdot\dfrac{2\log x}{x}dx\\
=x(\log x)^2-2\displaystyle\int \log xdx$

$\log x$ を積分するために、もう一度部分積分を使います：
$x(\log x)^2-2\displaystyle\int 1\cdot\log xdx$
$=x(\log x)^2$$-2(x\log x-\displaystyle\int x\cdot\dfrac{1}{x}dx)$
$=x(\log x)^2-2x\log x+2x+C$

グラフ

$y=(\log x)^2$ のグラフの概形を書いてみましょう。

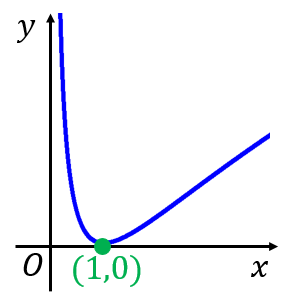
$\log x$ が $-\infty$ から $\infty$ まで単調増加することを考えると、$y=(\log x)^2$ のグラフは以下のようになります（増減表を書く必要はありません）。

～グラフを書くときのポイント～
・定義域は $x>0$、値域は $y\geq 0$ です。
・漸近線は $y$ 軸（$x=0$）です。
・$x=1$ で $y=0$ となります（$x$ 軸と交わる）。それより前は減少、それ以降は増加します。

次回は sin2x、cos2x、tan2xの微分 を解説します。