分数の足し算は、分母が同じ場合、分子だけ足し算をします。
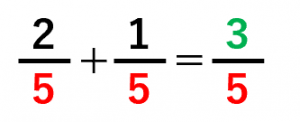
このページでは
・分数の足し算や引き算はどうやるのか?
・分母が違う場合どうするのか?
といった、分数の足し引きについての疑問にお答えします。
分母が同じ分数の足し算
を計算してみましょう。
$\dfrac{2}{5}$ と $\dfrac{1}{5}$ は、分母がどちらも $5$ で同じです。このように、分母が同じである分数の足し算は、分子を足し算します。
$\dfrac{2}{5}+\dfrac{1}{5}=\dfrac{2+1}{5}=$$\dfrac{3}{5}$
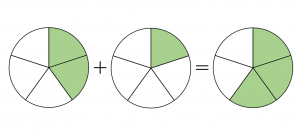
なぜ分子を足せばよいのかは図を見ればわかりやすいです。この場合「5個に分けた2つぶん」と「5個に分けた1つぶん」を加えると「5個に分けた3つぶん」になる、と説明できます。
分母が同じ分数の引き算
を計算してみましょう。
引き算の場合も分子を引き算すればOKです:
$\dfrac{5}{8}-\dfrac{3}{8}=\dfrac{5-3}{8}=\dfrac{2}{8}$
さらに、答えを約分すると、
$\dfrac{2}{8}=$$\dfrac{1}{4}$
となります。
→約分のやり方と計算ツール
分母が違う場合
通分のやり方が分からない場合は、先に通分のやり方と練習問題をやることをおすすめします。
を計算してみましょう。
分母が $3$ と $2$ で異なるので、まずは通分します:
$\dfrac{1}{3}+\dfrac{1}{2}=\dfrac{2}{6}+\dfrac{3}{6}$
分母が同じになったので、分子を足し算します:
$\dfrac{2}{6}+\dfrac{3}{6}=\dfrac{5}{6}$
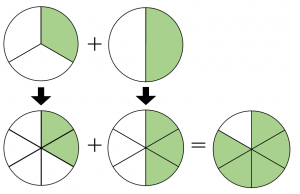
これも図を見ればわかりやすいです。
複雑な計算問題
を計算してみましょう。
引き算が入っても、項の数が増えてもやることは同じです。
まず通分します:
$\dfrac{2}{3}-\dfrac{1}{5}+\dfrac{1}{2}=\dfrac{20}{30}-\dfrac{6}{30}+\dfrac{15}{30}$
次に、分子を足し引きします:
$\dfrac{20-6+15}{30}=\dfrac{29}{30}$
次回は 分数のかけ算のやり方と例題5問 を解説します。
