正四角錐の定義、展開図、表面積、体積について解説します。
正四角錐の定義

正四角錐は、四角錐の中でも特別対称性が高く、きれいな立体です。
なお、側面が全て二等辺三角形であるという条件は、(山頂部にある)頂点から底面に下ろした垂線の足が、正方形の真ん中(重心)にある、と言い換えることもできます。
正四角錐の展開図
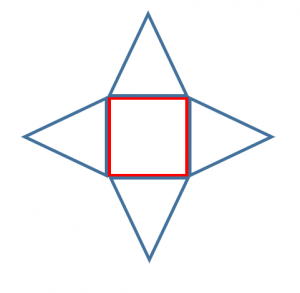
正四角錐の展開図は図のようになります。正方形1枚と二等辺三角形4枚でできています。
辺の長さによって、細長い形のものもあれば、つぶれた形のものもあります。
正四角錐の表面積
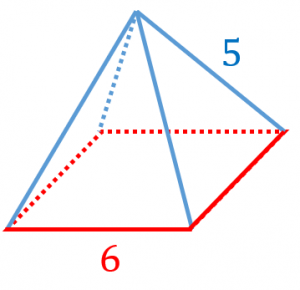
底面積は、正方形の面積 なので、$6\times 6=36$ です。
側面積は、図のような二等辺三角形 $4$ 枚分の面積です。
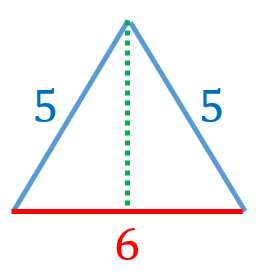
二等辺三角形の高さは、三平方の定理より、
$\sqrt{5^2-3^2}=4$
になります。
よって、側面積は、
$6\times 4\times\dfrac{1}{2}\times 4=48$
となります。
表面積は、底面積 $+$ 側面積なので、
$36+48=84$
になります。
正四角錐の体積
高さが分かっている正四角錐の体積は、四角錐の体積を求める公式を使って計算することができます。高さが分かっていない場合は、三平方の定理が必要になるので、中学数学レベルになります。

体積を求めるためには、正四角錐の高さ $AH$ を求める必要があります。
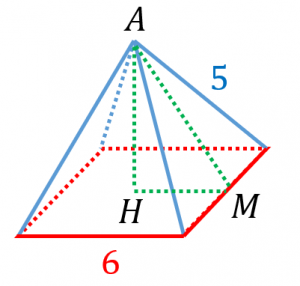
そこで、三角形 $AHM$ について考えてみます。
ただし、$M$ は底面を構成する辺の中点です。
$\angle AHM$ は直角で、$HM=3$ です。
また、$AM=4$ です(先ほど側面積を求める際に求めました)。
よって、三角形 $AHM$ に三平方の定理を使うと、
$AH=\sqrt{4^2-3^2}=\sqrt{7}$
になります。
したがって、正四角錐の体積は、
$6\times 6\times \sqrt{7}\times\dfrac{1}{3}=12\sqrt{7}$
となります。
次回は 円錐の側面積、底面積、表面積の求め方 を解説します。
