$\sin 15^{\circ}=\dfrac{\sqrt{6}-\sqrt{2}}{4}$
$\cos 15^{\circ}=\dfrac{\sqrt{6}+\sqrt{2}}{4}$
$\tan 15^{\circ}=2-\sqrt{3}$
$\sin 15^{\circ}$ の導出方法
三角関数の加法定理:
$\sin (\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$
を使うと、
$\sin 15^{\circ}\\
=\sin (60^{\circ}-45^{\circ})\\
=\sin 60^{\circ}\cos 45^{\circ}-\cos 60^{\circ}\sin 45^{\circ}\\
=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{2}-\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\\
=\dfrac{\sqrt{6}-\sqrt{2}}{4}$
となります。
ちなみに、半角の公式を使っても $\sin 15^{\circ}$ を計算することができます。(半角の公式の使い方、導出、覚え方の例題1)
$\cos 15^{\circ}$ の導出方法
加法定理:
$\cos (\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$
を使うと、
$\cos 15^{\circ}\\
=\cos (60^{\circ}-45^{\circ})\\
=\cos 60^{\circ}\cos 45^{\circ}+\sin 60^{\circ}\sin 45^{\circ}\\
=\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{2}\\
=\dfrac{\sqrt{6}+\sqrt{2}}{4}$
となります。
$\tan 15^{\circ}$ の導出方法
加法定理:
$\tan(\alpha-\beta)=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}$
を使うと、
$\tan 15^{\circ}\\
=\tan (60^{\circ}-45^{\circ})\\
=\dfrac{\tan 60^{\circ}-\tan 45^{\circ}}{1+\tan 60^{\circ}\tan 45^{\circ}}\\
=\dfrac{\sqrt{3}-1}{1+\sqrt{3}\cdot 1}\\
=2-\sqrt{3}$
となります。ただし、最後で分母の有理化を行いました。
直角三角形を用いた導出
図のような直角三角形を考えます。
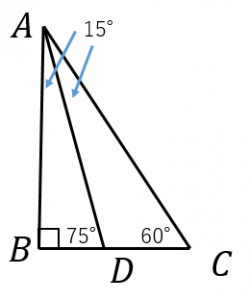
求めたいのは、$\tan 15^{\circ}=\dfrac{BD}{AB}$ です。
$BC=x$ とおくと(三角形 $ABC$ は $30^{\circ}$ の角を持つ直角三角形なので)$AC=2x$、$AB=\sqrt{3}x$ です。
また、角の二等分線定理より、
$BD:DC=AB:AC=\sqrt{3}:2$ です。
よって、$BD=\dfrac{\sqrt{3}}{\sqrt{3}+2}x$ となります。
以上より、$\tan 15^{\circ}=\dfrac{\frac{\sqrt{3}}{\sqrt{3}+2}x}{\sqrt{3}x}=2-\sqrt{3}$
となります(ここから $\sin 15^{\circ}$、$\cos 15^{\circ}$ の値を求めるのも簡単です)。
sin75度、cos75度、tan75度などの値
$\sin 75^{\circ}=\cos 15^{\circ}=\dfrac{\sqrt{6}+\sqrt{2}}{4}$
$\cos 75^{\circ}=\sin 15^{\circ}=\dfrac{\sqrt{6}-\sqrt{2}}{4}$
$\tan 75^{\circ}=\dfrac{1}{\tan 15^{\circ}}=2+\sqrt{3}$
$\sin 105^{\circ}=\sin 75^{\circ}=\dfrac{\sqrt{6}+\sqrt{2}}{4}$
$\cos 105^{\circ}=-\cos 75^{\circ}=\dfrac{-\sqrt{6}+\sqrt{2}}{4}$
$\tan 105^{\circ}=-\tan 75^{\circ}=-2-\sqrt{3}$
次回は 座標平面上における回転の公式 を解説します。
