正三角形の内接円の半径と外接円の半径

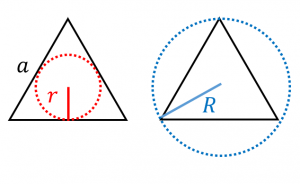
いろいろな方法で計算してみます。

直角三角形を使う方法

正三角形の中心を $O$ とおき、$BC$ の中点を $M$ とおくと $OM$ は内接円の半径 になります。

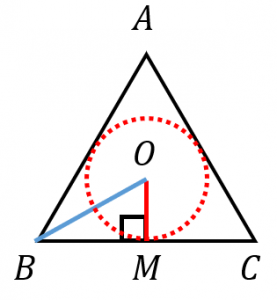
三角形 $BMO$ は、$30^{\circ},60^{\circ},90^{\circ}$ の直角三角形なので、辺の長さの比は $1:2:\sqrt{3}$ になります。よって、内接円の半径は、
$OM=\dfrac{1}{\sqrt{3}}BM\\
=\dfrac{1}{\sqrt{3}}\times\dfrac{1}{2}BC\\
=\dfrac{\sqrt{3}}{6}a$
となります。

$BO$ は外接円の半径になるので、外接円の半径は、
$BO=\dfrac{2}{\sqrt{3}}BM\\
=\dfrac{1}{\sqrt{3}}BC\\
=\dfrac{\sqrt{3}}{3}a$
となります。

重心を使う方法

対称性より、正三角形では、
・内接円の中心
・外接円の中心
・重心
が全て一致します。

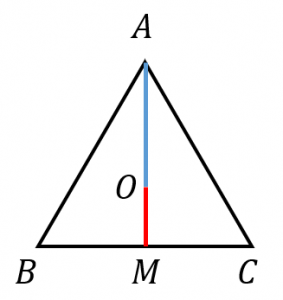
重心 $O$ が、中線を $2:1$ に内分することを使うと、
内接円の半径は
$OM=\dfrac{1}{3}AM\\
=\dfrac{1}{3}\times\dfrac{\sqrt{3}}{2}AB\\
=\dfrac{\sqrt{3}}{6}a$
となります。

同様に、外接円の半径は
$OG=\dfrac{2}{3}AM\\
=\dfrac{\sqrt{3}}{3}a$
となります。

三角形の面積を使って内接円の半径を求める

内接円の半径を $r$ とおきます。
内接円の半径を求める公式より、
$r=\dfrac{2S}{a+b+c}$
です。また、正三角形の面積の求め方より、$S=\dfrac{\sqrt{3}}{4}a^2$
が成立します。

よって、
$r=\dfrac{2\times\frac{\sqrt{3}}{4}a^2}{a+a+a}\\
=\dfrac{\sqrt{3}}{6}a$
になります。

正弦定理を使って外接円の半径を求める

外接円の半径を $R$ とおくと、正弦定理より、
$\dfrac{a}{\sin 60^{\circ}}=2R$
です。よって、
$R=\dfrac{a}{2\sin 60^{\circ}}\\
=\dfrac{a}{\sqrt{3}}\\
=\dfrac{\sqrt{3}}{3}a$
となります。

次回は 正方形の対角線の長さを求める方法 を解説します。