ヤング率の意味、ばね定数との違い

このページでは、ヤング率の意味を説明します。また、ヤング率とばね定数の共通点と違いについて分かりやすく解説します。

ヤング率とは

物体に力を加えると、変形します。このとき、
・(単位面積あたりにかかる)力の大きさ $\dfrac{F}{S}$ を応力度と言います。
・(単位長さあたりの)変形の大きさ $\dfrac{\Delta L}{L}$ をひずみと言います。

参考：ひずみとポアソン比について分かりやすく解説

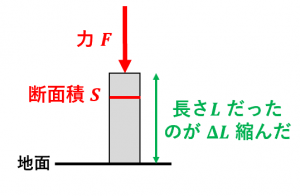
加えた力が小さいとき、応力度 $\sigma$ はひずみ $\varepsilon$ に比例します：
$\sigma =E\varepsilon$
この比例定数 $E$ がヤング率です。

ヤング率が大きいほど、力を加えてもあまり変形しない。つまり「硬い」材質と言うことができます。

ヤング率とばね定数の関係

フックの法則：
$F=kx$
力の大きさ $F$ が小さい時、$F$ は、ばね（材料）の伸びた長さ $x$ に比例します。比例定数 $k$ がばね定数です。

ヤング率の定義式：
$\sigma =E\varepsilon$
応力度 $\sigma$ が小さい時、$\sigma$ はひずみ $\varepsilon$ に比例します。比例定数 $E$ がヤング率です。

ただし、$L$ は材料の（力を加えていない状況における）長さで、$S$ は断面積です。

この関係式を証明してみます。
ヤング率の定義式に、
$\sigma=\dfrac{F}{S}$、$\varepsilon=\dfrac{x}{L}$ という関係式（応力度、ひずみの定義式）を使うと、
$\dfrac{F}{S}=E\dfrac{x}{L}$
となります。さらにフックの法則を使うと、
$\dfrac{k}{S}=E\dfrac{1}{L}$
$k=\dfrac{S}{L}E$
となります。

ヤング率とばね定数の違い

ヤング率とばね定数の共通点
どちらも、物体の「硬さ」を表す定数です。数値が大きいほど、力を加えても変形しにくいと言えます。

ヤング率とばね定数の違い
ヤング率は素材に固有の定数です。大きさや断面積に依存しません。
一方、ばね定数は、素材が同じでも、大きさや断面積が違えば異なります。

「大きい鉄のばね」と「小さい鉄のばね」では、ヤング率は同じですが、ばね定数は異なります。

次回は パリティビットの意味と誤り検出、誤り訂正の方法 を解説します。