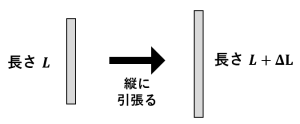
ひずみとは(単位長さあたり)物体がどれくらい伸びたり縮んだりしているかを表す指標です。
長さ $L$ の物体を引張って $L+\Delta L$ になったときのひずみは、$\dfrac{\Delta L}{L}$ です。
ひずみは構造力学・材料力学における基本的な用語です。このページでは、ひずみやポアソン比について、分かりやすく解説します。
ひずみの計算例
ひずみの定義 $\dfrac{\Delta L}{L}$ を使うと、
$\dfrac{2}{50}=0.04$
となります。
ひずみは、$\varepsilon$ という記号を使って表すことが多いです。$\varepsilon$ はイプシロンと読みます。
ひずみの単位
もう少し正確に言うと、ひずみは長さを長さでったものなので、無次元量です。
ただし、ひずみであることを表すために、数字の後ろに $\varepsilon$ をつけることがあります。つまり、上の例題では「ひずみは $0.04$」と言うことも「ひずみは $0.04\:\varepsilon$」と言うこともあります。
ひずみの符号
物体を引張って伸ばした場合には、$\Delta L>0$ なので、ひずみはプラスです。引張ひずみと言います。
一方、物体を押しつぶして圧縮した場合には、$\Delta L <0$ なので、ひずみはマイナスです。圧縮ひずみと言います。
縦ひずみと横ひずみ
ここまでは、物体を引張ったり圧縮したりした方向のひずみを考えました。これを縦ひずみと言います。
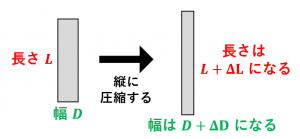
一方、力を加えた方向から見て横の方向についても、ひずみを考えることができます。
つまり、圧縮前の幅を $D$ とし、圧縮した後の幅を $D+\Delta D$ とすると、横の方向のひずみは、$\dfrac{\Delta D}{D}$ と定義されます。これを横ひずみと言います。図では $\Delta D<0$ なので、横ひずみはマイナスです。
ポアソン比
つまり、ポアソン比は $-\dfrac{\varepsilon_2}{\varepsilon_1}$ で定義されます。
※一般的に縦ひずみと横ひずみの符号は逆なので、比率を $-1$ 倍したものを考えることで、ポアソン比が(一般的に)プラスになるようにしています。
ポアソン比は、物質・材料に固有の定数です。つまり、ひずみの大きさによらず、$-\dfrac{\varepsilon_2}{\varepsilon_1}$ で一定です。一般的に、ポアソン比は $0$ 以上 $\dfrac{1}{2}$ 以下の値を取ります(例外的にマイナスになることもあります)。
大雑把には、ポアソン比が大きい($\dfrac{1}{2}$ に近い)物質は、縦にひずませると、潰されずに横に膨張すると言えます。
逆に、ポアソン比が小さい($0$ に近い)物質は、縦にひずませると、圧縮されるだけで横には膨張しないと言えます。
次回は ヤング率の意味、ばね定数との違い を解説します。
