数学において、パリティとは、偶奇性(偶数なのか奇数なのかを表す言葉)のことです。
パリティビットとは、$1$ の数が偶数か奇数かによって、末尾にくっつけるビットのことです。パリティビットを使うことで、誤り検出や誤り訂正を実現できます。
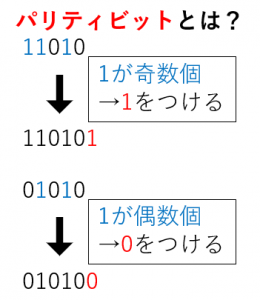
パリティビットとは
コンピュータの世界では、情報を $0$ と $1$ で表現します。
例えば、$010$ や $110100010$ という情報を送りたいとします。
~例1~
$010$ という情報を送りたい
→ $1$ が奇数個(1個)なので、末尾に $1$ をつける
→ $0101$ ($1$ の数が偶数個になった)を送る
~例2~
$110100010$ を送りたい
→ $1$ が偶数個(4個)なので、末尾に $0$ をつける
→$1101000100$ ($1$ の数は偶数個のまま)を送る
パリティチェックと誤り検出方法
~具体例~
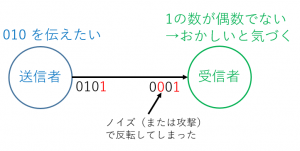
・送信者は $010$ を送りたい
・パリティビットを加えて $0101$ を送る
・(例えば3桁目にノイズが乗ってしまうと)受信者には $0001$ と伝わってしまう
・受信者は $1$ の数が偶数でないのでおかしいと気づく→再送をお願いする→正しい情報を得ることができる!
このように、受信者が $1$ の数が偶数個かどうかを確認する計算をパリティチェックと言います。
誤り訂正方法
先ほどの誤り検出方法では「どこかで間違いが起きた」と分かっても、どこのビットで間違いが起きたのかは分かりません(復元はできない)。
そこで、さらに余分な情報をつけ加えることで誤り訂正もできるようになります。
~具体例~
・送信者は $110100010$ を送りたい
・途中で改行をはさんで
$110$
$100$
$010$
という情報にしてみる。
・各行と各列、それぞれにパリティビットをつけて(各行、各列の $1$ の数が偶数個になるようにして)送る:
$110$$0$
$100$$1$
$010$$1$
$000$
・万一真ん中の $0$ が反転した場合、受信者には
$1100$
$1$$1$$01$
$0101$
$000$
と伝わる。
・二行目と二列目の1の数が奇数でおかしいので、受信者は、そこが間違いだったと気づくことができる!
次回は バーナム暗号の意味と広く使われていない理由 を解説します。
