最終更新日 2018/02/05
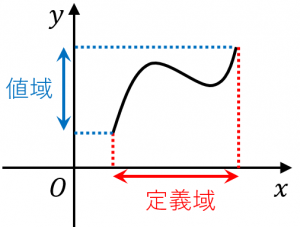
関数 $y=f(x)$ について、
$x$ がとりうる値の範囲のことを定義域
$y$ がとりうる値の範囲のことを値域
と言います。
また、定義域と値域を合わせて変域と言います。
※値域は「ちいき」と読みます。
一次関数の例題
定義域、値域に関する問題では、関数のグラフを書くようにしましょう。
$y=2x-2\:(1\leq x\leq 3)$ という一次関数の値域を求めてみましょう。
解答
定義域は $1\leq x\leq 3$ です。
この範囲で、$y=2x-2$ のグラフを書いてみると、図のようになります。
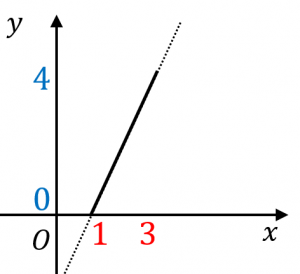
$x=1$ のとき $y=0$
$x=3$ のとき $y=4$
です。よって $y$ のとりうる値の範囲は $0\leq y\leq 4$ です。
つまり、値域は $0\leq y\leq 4$ です。
二次関数の例題
次は、二次関数の最大値・最小値に関連した高校数学レベルの問題です。
二次関数 $y=-2x^2+12x-3\:(0< x\leq 4)$ における値域を求めてみましょう。
まずは、グラフを書くために、平方完成します：
$y=-2(x^2-6x)-3$
$y=-2(x^2-6x+9-9)-3$
$y=-2(x-3)^2+15$
よって、頂点が $(3,15)$ になることに注意してグラフを書くと、図のようになります。
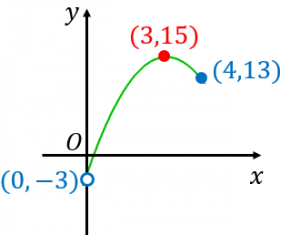
グラフの両端は $(0,-3)$、$(4,13)$ です。ただし、$(0,-3)$ はギリギリ範囲の外です。
よって、値域は、$-3< y\leq 15$ です。
まとめ
・定義域：入力 $x$ のとりうる値の範囲
・値域：出力 $y$ のとりうる値の範囲
・変域：定義域と値域を合わせて変域と呼ぶ
・一次関数でも、二次関数でも、より複雑な関数でも、グラフを書くことで、変域を求めることができる。
次回は 二次関数の最大値と最小値を求める問題4問 を解説します。
