・主成分分析における「主成分」について、2つの意味を説明します。
・2つの意味のうちどちらを使っても、主成分がデータの分散共分散行列の固有ベクトルに対応することを証明します。
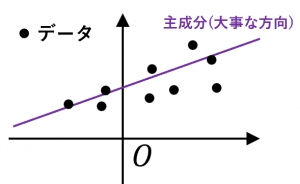
主成分とは
「大事な方向」とは、
1. データの分散が最大になる方向
2. 直線上の点でデータを近似したときに、その近似の二乗誤差が最小になるような最適な直線の方向
のことです。
なんと、上の2つの意味での「大事な方向」は一致します。つまり、第一主成分は、上記の同値な2つの定義があります。
※このページでは、わかりやすさを重視して、第一主成分のみを用いた説明をします。第二主成分以降も同様に固有値問題に帰着できます。
データの分散から主成分の導出
1. データの分散が最大になる方向
を計算してみましょう。
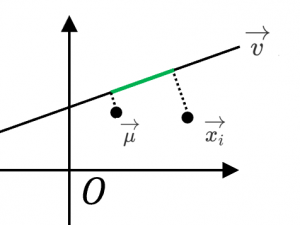
求める方向を、単位ベクトル $\overrightarrow{v}$ を使って表します。→方向ベクトルの意味と2通りの求め方
データを $\overrightarrow{x_1},\dots,\overrightarrow{x_n}$、その平均ベクトルを $\overrightarrow{\mu}=\dfrac{1}{n}\displaystyle\sum_{i=1}^n\overrightarrow{x_i}$
とします。
$\overrightarrow{v}$ 方向の分散とは、$\overrightarrow{v}$ 方向成分の偏差(図の緑色の線分に対応)の二乗の和なので、
$\displaystyle\sum_{i=1}^n(\overrightarrow{v}\cdot(\overrightarrow{x_i}-\overrightarrow{\mu}))^2\\
=\overrightarrow{v}^{\top}\Sigma\overrightarrow{v}$
となります(注1)。ただし、$\Sigma$ は分散共分散行列です。
この二次形式(多変数の二次関数)
$\overrightarrow{v}^{\top}\Sigma\overrightarrow{v}$
を最大にするような $\overrightarrow{v}$
は、$\Sigma$ の最大固有値に対応する固有ベクトルであることが知られています(注2)。
つまり、第一主成分とは、データの分散共分散行列の最大固有値に対応する固有ベクトルです。
注1:この等号は、少し難しいですが、分散共分散行列の定義を理解した上で、データ数と次元がともに $2$ の場合などで具体的に書き下すと理解できます。
注2:Courant–Fischer の最大・最小定理
「近似誤差最小」から主成分の導出
2. 直線上の点でデータを近似したときに、その近似誤差が最小になるような最適な直線の方向
を計算してみましょう。
データを $\overrightarrow{v}^{\top}\overrightarrow{x}+b=0$ という直線上の点で近似するとしましょう。
ただし、全体を定数倍しても式が表す直線は変わらないので、$\overrightarrow{v}$ は単位ベクトルとします。
データ $\overrightarrow{x_i}$ をこの直線上の点で近似したときの二乗誤差は、点と直線の距離公式より、
$(\overrightarrow{v}^{\top}\overrightarrow{x_i}+b)^2$
となります。よって、
$\displaystyle\sum_{i=1}^n(\overrightarrow{v}^{\top}\overrightarrow{x_i}+b)^2$
を最小にする $\overrightarrow{v},b$ を求めた際の $\overrightarrow{v}$ が2の意味での第一主成分になります。
まず、$\overrightarrow{v}$ を固定して $b$ の最小値を求めると、
(高校数学で習う一変数の二次関数の最小化問題を解いて)
$b=-\dfrac{1}{n}\displaystyle\sum_{i=1}^n\overrightarrow{v}^{\top}\overrightarrow{x_i}\\
=-\overrightarrow{v}^{\top}\overrightarrow{\mu}$
となります。
よって、
$\displaystyle\sum_{i=1}^n(\overrightarrow{v}^{\top}(\overrightarrow{x_i}-\overrightarrow{\mu}))^2$
を最小にする $\overrightarrow{v}$ が第一主成分になります。
実は、この式は1の意味での主成分を計算したときに出てきた$\overrightarrow{v}$ 方向の偏差の二乗の和と一致しています。
つまり、2. 直線上の点でデータを近似したときに、その近似誤差が最小になるような最適な直線の方向は、データの分散共分散行列の最大固有値に対応する固有ベクトルであることが分かりました。
次回は 回帰分析の意味、嬉しさ、関連する用語 を解説します。
