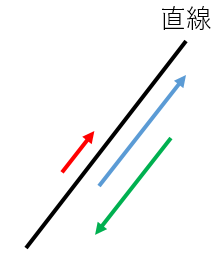
直線が与えられたとき、それと同じ「方向」を向いたベクトルのことを方向ベクトルと言う。
直線に対して、赤いベクトルも青いベクトルも緑のベクトルも全て方向ベクトル(長くても、短くても、逆向きでも方向ベクトル)。
方向ベクトルの求め方
例題1:
直線 $y=2x+3$ の方向ベクトルを1つ求めよ。
考え方1
2点 $\overrightarrow{a}$ と $\overrightarrow{b}$ を通る直線の方向ベクトルの1つは、$\overrightarrow{a}-\overrightarrow{b}$ です。
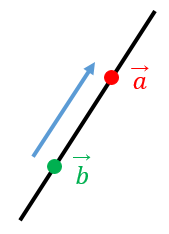
よって、通る2点が分かれば方向ベクトルが計算できます。
さて、この直線の式に $x=0$ と $x=1$ を代入すると、$(0,3)$ と $(1,5)$ を通ることが分かります。よって、方向ベクトルは、$\begin{pmatrix}1-0\\5-3\end{pmatrix}=\begin{pmatrix}1\\2\end{pmatrix}$
考え方2
傾きが $2$ なので、$x$ が $1$ 増加すると、$y$ は $2$ 増加します。よって、方向ベクトルは、$\overrightarrow{t}=\begin{pmatrix}1\\2\end{pmatrix}$
ax+by+c=0 タイプの場合
例題2:$ax+by+c=0$ の方向ベクトルを1つ求めよ。
考え方1
$ax+by+c=0$ の法線ベクトル(直線と垂直なベクトル)の1つは、$\overrightarrow{n}=\begin{pmatrix}a\\b\end{pmatrix}$ です。
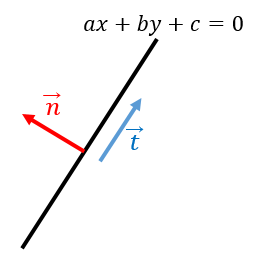
よって、方向ベクトルを $\overrightarrow{t}=\begin{pmatrix}x\\y\end{pmatrix}$ とおくと、$\overrightarrow{n}\cdot\overrightarrow{t}=0$ となります。
つまり、$ax+by=0$ です。
ここで、$x=-b$、$y=a$ とすれば上の式を満たします。よって、方向ベクトルの1つは、
$\overrightarrow{t}=\begin{pmatrix}-b\\a\end{pmatrix}$
となります。
考え方2($a$ も $b$ も $0$ でないときに使える)
この直線は $(0,-\frac{c}{b})$ と $(-\frac{c}{a},0)$ を通ります。よって、方向ベクトルは、$\begin{pmatrix}-\frac{c}{a}-0\\0-(-\frac{c}{b})\end{pmatrix}=\begin{pmatrix}-\frac{c}{a}\\\frac{c}{b}\end{pmatrix}$
方向ベクトルは定数倍しても方向ベクトルなので、見やすくするために $\dfrac{ab}{c}$ 倍すると、
$\overrightarrow{t}=\begin{pmatrix}-b\\a\end{pmatrix}$
となります。
まとめ
・$y=ax+b$ の方向ベクトルの1つは、$\begin{pmatrix}1\\a\end{pmatrix}$
・$ax+by+c=0$ の方向ベクトルの1つは、$\begin{pmatrix}-b\\a\end{pmatrix}$
・2点 $\overrightarrow{p}$ と $\overrightarrow{q}$ を通る直線の方向ベクトルの1つは、$\overrightarrow{p}-\overrightarrow{q}$
・方向ベクトルを定数倍したものも方向ベクトル。
次回は 内積の意味と3つの公式 を解説します。
