回帰分析の意味、嬉しさ、関連する用語

具体例

各日の来客数 $x$（人） と売上 $y$（万円） のデータが10日ぶんあるとします：
$(x,y)$
$=(10,3),(30,9),(45,14),(36,11),(20,6)$
$,(60,18),(50,15),(42,13),(35,13),(24,8)$

これをプロットしたのが図の青い点です。

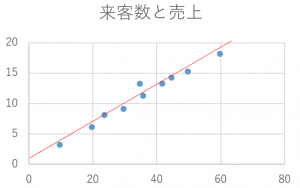
青い点は図の赤い直線付近にあることが分かります！このように、データ（青い点）があるときに、それっぽい関係式（赤い線）を予測するのが回帰分析です。（具体的に赤い直線の式を求める方法は別記事で解説します）

回帰分析の嬉しさ

回帰分析をすることで、「それっぽい関係式」$y=f(x)$ （上の例では赤い直線）が得られます。

この関係式をもとに、新しい入力に対して出力がどれくらいか予測することができます。上の例では、来客数が分かれば売上が予測できます。 例えば、新たに、ある日の来客数が $40$ 人であることが分かれば売上はだいたい $13$ 万円であることが推定できます。

このように、回帰分析は、手元のデータをもとに、関係式を立てて、未知の事柄について推定する手法と言えます。

回帰分析のモデルとは

$x$ と $y$ の間の「それっぽい関係式」を求めるという目標は抽象的です。そこで「それっぽい関係式」の候補を限定した上で、その候補の中から一番それっぽいものを選ぶ、という手法が取られます。この「それっぽい関係式の候補たち」を回帰分析のモデル（または回帰モデル）と言います。

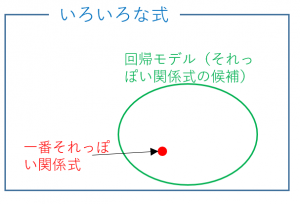
多くの場合、回帰モデルを立てるのは人間の仕事、そこから一番それっぽい関係式を見つけるのは計算ソフト（エクセルとか）の仕事です。

例えば、$x$ と $y$ の間の直線的な関係を仮定して、$y=ax+b$ という回帰モデルの元で考える、ということをよくやります。

回帰分析に関連する用語

入力側の変数 $x$ を独立変数（または説明変数）と言います。出力側の変数 $y$ を従属変数（または被説明変数、目的変数）と言います。

独立変数が一つであるような回帰分析を単回帰分析と言います。例えば、$y=ax+b$ の $a$ と $b$ を推定したい、という問題は単回帰分析です。（最も基本的）

独立変数が二つ以上であるような回帰分析を重回帰分析と言います。例えば、$y=ax_1+bx_2+c$ の $a,b,c$ を推定したい、という問題は重回帰分析です。

また、$\log \dfrac{y}{1-y}=ax+b$ という回帰モデルをロジスティック回帰モデルと言います。（二値分類問題など、幅広い応用あり）
左辺はロジット関数と呼ばれる関数です。

次回は 重回帰分析における係数の意味と求め方 を解説します。