垂直二等分線の方程式の求め方を２通り解説

座標平面上で、垂直二等分線を求める方法を２通り解説します。

方法１

$A(1,3),B(5,1)$ とするとき、$AB$ の垂直二等分線の方程式を計算してみましょう。

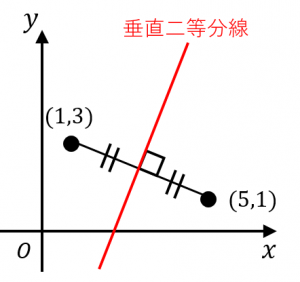
１．通る１点を求める
$AB$ の中点の座標は、$\left(\dfrac{1+5}{2},\dfrac{3+1}{2}\right)=(3,2)$ です。つまり、垂直二等分線は $(3,2)$ を通ります。

２．傾きを求める
直線 $AB$ の傾きは、$\dfrac{1-3}{5-1}=-\dfrac{1}{2}$ です。よって、垂直二等分線の傾きを $m$ とすると、$m\times\left(-\dfrac{1}{2}\right)=-1$ です。
よって、$m=2$ となります。
（垂直な二直線の傾きの積は $-1$ になることを使いました）

３．直線の式を求める
以上より、通る１点の座標と傾きが分かったので、垂直二等分線の方程式は、
$y-2=2(x-3)$
つまり、
$y=2x-4$
となります。

～補足～
・中点の座標を求める公式と証明
・傾きと切片の意味と求め方を丁寧に解説

方法２

$AB$ の垂直二等分線は、$A$ と $B$ からの距離が等しい点の集合です。

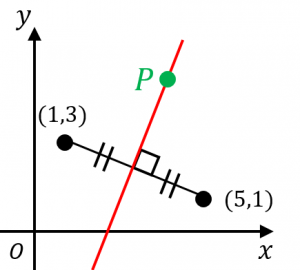
$P(x,y)$ が $AB$ の垂直二等分線上にある必要十分条件は、$PA=PB$ です。
つまり、
$(x-1)^2+(y-3)^2\\
=(x-5)^2+(y-1)^2$
です。これを展開して整理していくと、
$-2x+1-6y+9=-10x+25-2y+1$
$-2x-6y+10=-10x-2y+26$
$-4y=-8x+16$
$y=2x-4$
となります。つまり、垂直二等分線の方程式は、
$y=2x-4$
です。

一般的な公式

先ほど説明した方法２を使って、この公式を証明してみます。

$P(x,y)$ が $AB$ の垂直二等分線上にある必要十分条件は、$PA=PB$ です。
つまり、
$(x-x_1)^2+(y-y_1)^2\\
=(x-x_2)^2+(y-y_2)^2$
です。これを展開して整理していくと、
$-2x_1x+x_1^2-2y_1y+y_1^2\\
=-2x_2x+x_2^2-2y_2y+y_2^2$
$(x_2-x_1)x+(y_2-y_1)y\\
=\dfrac{1}{2}(x_2^2-x_1^2+y_2^2-y_1^2)$
となります。

次回は 中点連結定理とその逆の証明および例題 を解説します。