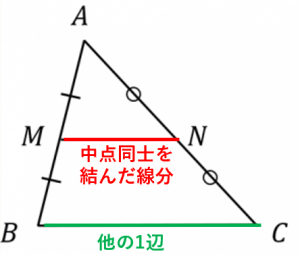
中点連結定理とその逆の証明および例題

このページでは、中点連結定理について
・中点連結定理とは何か？
・中点連結定理の証明方法は？
・中点連結定理を使う問題はどうやって解くのか？
といった疑問にお答えします。

中点連結定理とは

中点連結定理とは、
「中点同士を結んだ線分は、他の1辺と平行で、長さが半分になる」
という定理です。

もう少しきちんと言うと、$M$ を $AB$ の中点、$N$ を $AC$ の中点とするとき、
・$2MN=BC$
・$MN$ と $BC$ は平行
が成立する、というのが中点連結定理です。

中点連結定理の証明

図において、三角形 $AMN$ と $ABC$ に注目します。

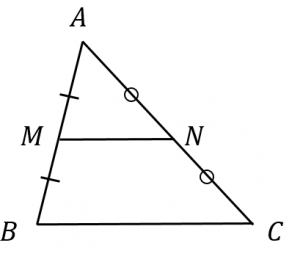
・$AM:AB=1:2=AN:NC$
・$\angle A$ が共通（$\angle MAN=\angle BAC$）

より、二辺の比とその間の角がそれぞれ等しいので、三角形 $AMN$ と $ABC$ は相似になります。
相似比は $1:2$ なので、$2MN=BC$ となります。

また、相似な三角形の対応する角は等しいので、$\angle AMN=\angle ABC$ です。よって、同位角が等しいので、$MN$ と $BC$ が平行であることが分かります。

中点連結定理を使った例題

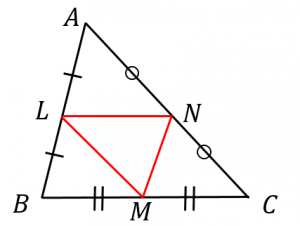
解答：
$L$ は $AB$ の中点、$N$ は $AC$ の中点なので、中点連結定理より、$LN=\dfrac{1}{2}BC$

同様に、
$LM=\dfrac{1}{2}AC$、$MN=\dfrac{1}{2}AB$

よって、三角形 $LMN$ の周の長さは、
$LN+LM+MN\\
=\dfrac{1}{2}(BC+AC+AB)\\
=\dfrac{1}{2}\cdot 12\\
=6$

中点連結定理の逆とその証明

つまり、

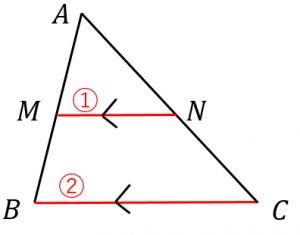
$AB$ 上の点 $M$ と $AC$ 上の点 $N$ が
・$2MN=BC$
・$MN$ と $BC$ は平行
を満たすとき、$M$ は $AB$ の中点、$N$ は $AC$ の中点
が成立します。

・平行線の同位角は等しいので、$\angle AMN=\angle ABC$
・同じく同位角より、$\angle ANM=\angle ACB$
よって、３つの角がそれぞれ等しいので、三角形 $AMN$ と $ABC$ は相似になります。

また、仮定より $MN:BC=1:2$ なので、相似比は $1:2$ です。よって、$AM:AB=1:2$ となります。つまり、$AM=MB$ となり、$M$ が $AB$ の中点であることが分かりました。

同様に、$AN:AC=1:2$ から $N$ が $AC$ の中点であることも分かります。

次回は 角の二等分線定理（内角、外角それぞれ） を解説します。