$a$ と $b$ の相乗平均(または幾何平均)とは、$\sqrt{ab}$ のことです。
(ただし、$a$、$b$ は $0$ 以上の数です)

具体例、相加平均との関係
例えば、2つの数 $3$ と $12$ に対して、相乗平均は、$\sqrt{3\times 12}=\sqrt{36}=6$ となります。
一方、相加平均(算術平均、いわゆる普通の平均) は $\dfrac{3+12}{2}=7.5$ です。このように、相加平均は、必ず相乗平均の値以上になります。つまり、$\dfrac{a+b}{2}\geq\sqrt{ab}$ が成立します。→相加平均、相乗平均の不等式の意味と使い方
図形的な意味
~相乗平均を図示する3ステップ~
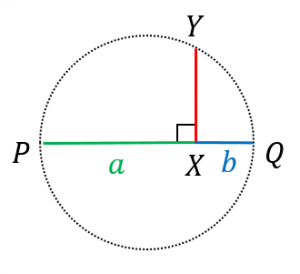
手順1:長さ $a$ の線分 $PX$、長さ $b$ の線分 $XQ$ をつなげて書きます。
手順2:$PQ$ を直径とする円を書きます。
手順3:$X$ を通り $PQ$ と垂直な直線と円の交点を $Y$ とします。線分 $XY$ の長さが、相乗平均 $\sqrt{ab}$ になります。
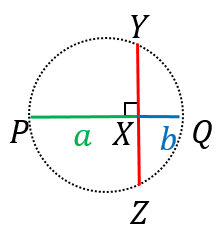
方べきの定理を使うと、$XY\times ZX=PX\times XQ=ab$ が分かります。$XY=ZX$ なので、$XY^2=ab$ つまり、$XY=\sqrt{ab}$ となります。
活躍する例
例題:$100$ 円だった物の価値が、1年目は $2$ %上がった。2年目は $18$ %上がった。この物の価値は年間平均何%上がったと言えるか?
この物の現在の価値は、$100\times 1.02\times 1.18=120.36$ 円になります。
平均成長率は、$\dfrac{2+18}{2}=10$ %と言いたくなります。しかし、もし、$100$ 円のものが2年とも $10$ %で成長した場合。現在の価値は、$100\times 1.1\times 1.1=121$ 円です。$120.36$ 円とは微妙にずれています。これでは平均とは言えません。
正しくは、2年間の成長率の相乗平均:$\sqrt{1.02\times 1.18}\simeq 9.71$ %が平均成長率になります。実際、2年とも $9.71$%で成長した場合、$100\times 1.0971\times 1.0971\simeq 120.36$ 円になります。
幾何平均と呼ぶこともある
相乗平均は、幾何平均と呼ばれることもあります。
「幾何」とは図形の性質を研究する数学の分野です。「幾何平均」は図形と関係があるため「幾何」と名付けられたと推測できます。
たくさんの数の相乗平均
より一般に、$x_1,\dots,x_n$ という $n$ 個の $0$ 以上の数に対して、相乗平均は
$\sqrt[n]{x_1\dots x_n}$
で定義されます。
次回は 繁分数式の問題と2通りの解き方 を解説します。
