双曲線に関する公式まとめ

双曲線に関する公式をまとめました。

$x$ 軸をまたぐ双曲線

$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$
は図のような $x$ 軸をまたぐ双曲線を表します。ただし、このページでは $a,b$ は正の数とします。

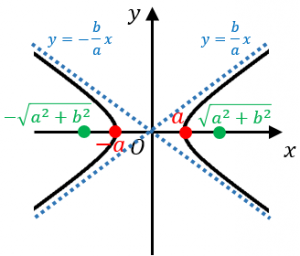
以下の4つの公式をセットで覚えておくとよいでしょう。
・$(-a,0),(a,0)$ を通る
・焦点の座標は $(-\sqrt{a^2+b^2},0)$ と $(\sqrt{a^2+b^2},0)$
・$y=\dfrac{b}{a}x$ と $y=-\dfrac{b}{a}x$ が漸近線
・双曲線上の点は、2点からの距離の差が $2a$ で一定

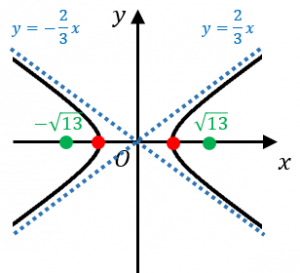
$a^2=9$、$b^2=4$ なので、$a=3$、$b=2$ として公式を使うと、
・$(-3,0),(3,0)$ を通る
・焦点の座標は $(-\sqrt{13},0)$ と $(\sqrt{13},0)$
・$y=\dfrac{2}{3}x$ と $y=-\dfrac{2}{3}x$ が漸近線

$y$ 軸をまたぐ双曲線

$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=-1$
は図のような $y$ 軸をまたぐ双曲線を表します。右辺が $-1$ か $+1$ かによって、向きが変わっています。

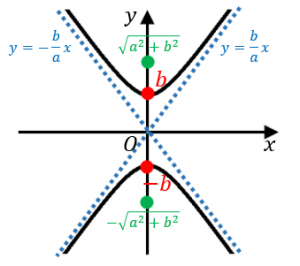
この場合、以下の4つの公式が成立します。
・$(0,-b),(0,b)$ を通る
・焦点の座標は $(0,-\sqrt{a^2+b^2})$ と $(0,\sqrt{a^2+b^2})$
・$y=\dfrac{b}{a}x$ と $y=-\dfrac{b}{a}x$ が漸近線
・双曲線上の点は、2点からの距離の差が $2b$ で一定

その他の公式

$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$
という双曲線上の点 $(x_0,y_0)$ における接線の方程式は、
$\dfrac{x_0x}{a^2}-\dfrac{y_0y}{b^2}=1$
となります。（右辺が $-1$ の場合、接線の方程式の右辺も $-1$ になります）

反比例のグラフ $y=\dfrac{k}{x}$ は、双曲線のグラフを回転させたものです。
関連：反比例の意味と身近な例４つ

さらに、極座標における双曲線の一般形は、
$r=\dfrac{l}{1+e\cos\theta}$
となります（ただし、$1 < e$ です）。

次回は 台形の重心を求める公式と導出 を解説します。