台形の重心を求める公式と導出

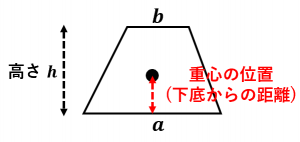
台形の重心を計算する公式の使い方と導出について詳しく解説します。

台形の重心を計算する具体例

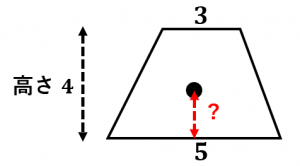
重心の下底からの距離は，
$\dfrac{a+2b}{3(a+b)}h\\
=\dfrac{5+2\cdot 3}{3(5+3)}\times 4\\
=\dfrac{11}{6}$
のように計算できます。

$\dfrac{11}{6}$ は $2$ よりも少しだけ小さいです。つまり「台形の重心は真ん中より少しだけ下側にある」という結果になり、直感的にも正しそうです。

台形の重心の導出

重心の定義は、断面一次モーメント÷面積です。

面積は、台形の面積を求める公式より、
$S=\dfrac{1}{2}(a+b)h$
です。

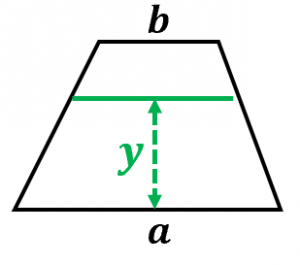
（下底まわりの）断面一次モーメントは、
$y$ における横棒の長さが $a+(b-a)\dfrac{y}{h}$ である(※)ので、
$M=\displaystyle\int_0^hy\left\{a+(b-a)\dfrac{y}{h}\right\}dy\\
=\dfrac{h^2a}{2}+(b-a)\dfrac{h^2}{3}\\
=\dfrac{a+2b}{6}h^2$
となります。

よって、重心の位置は
$M\div S=\dfrac{a+2b}{3(a+b)}h$
となります。

※ $y$ における横棒の長さは、$y=0$ のとき $a$ になり、$y=h$ のとき $b$ になるような、$y$ についての１次関数になります。

台形の重心公式について補足

$a=b$ のとき、重心の位置は $\dfrac{h}{2}$ となります。つまり、上底と下底の長さが等しい台形（つまり平行四辺形）の重心は、上底と下底のちょうど真ん中になります。

また、重心公式は $\dfrac{1}{2}-\dfrac{a-b}{6(a+b)}$ と変形することもできます。したがって、下底 $a$ が上底 $b$ より長い $\iff$ 台形の重心は上底よりも下底に近いという性質が成立します。

なお、台形の重心の位置のうち、縦方向（$y$ 方向）については公式を使うことで求めることができました。一方、横方向の位置を求めるには、重心の定義に従って積分計算をする必要があります。ただし、等脚台形の場合には左右対称なので、横方向の重心は真ん中にあり、計算するまでもありません。

次回は 半円の重心の位置を求める公式 を解説します。