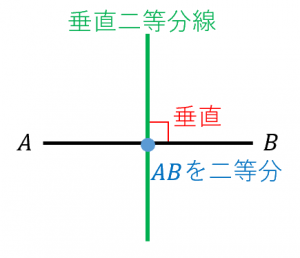
垂直二等分線とは、与えられた線分 $AB$ に対して「それと垂直であり」「二等分する」ような直線のことです。
このページでは、垂直二等分線の定義と作図方法を詳しく解説します。
垂直二等分線とは
線分 $AB$ に対して、
・それと垂直であり
・中点を通る(つまり、二等分する)
ような直線のことを垂直二等分線と言います。

垂直二等分線の作図方法
手順1.コンパスを使って $A$ を中心に、円を書く
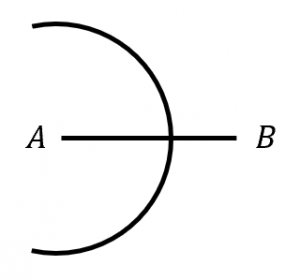
手順2.コンパスを使って $B$ を中心に、手順1と同じ半径の円を書く(※)
※2つの円が2点で交わるようなサイズの円を書きましょう。
※また、2つの円の交点さえ分かればよいので、円全体を書かなくても、一部分だけでもOKです。
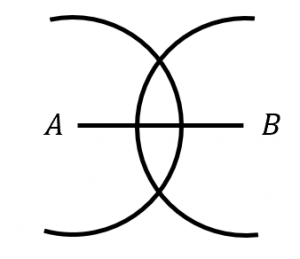
手順3.2つの円の交点が2つできる。定規を使ってこの2つの点を通る直線を引くと、垂直二等分線となる。
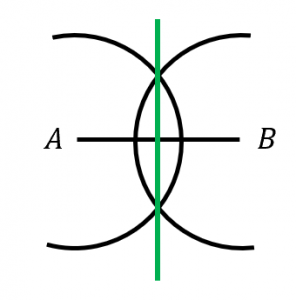
垂直二等分線の作図は、作図問題の中でも最も基本的なものの1つです。しっかりマスターしましょう。
上記の作図方法が正しい理由
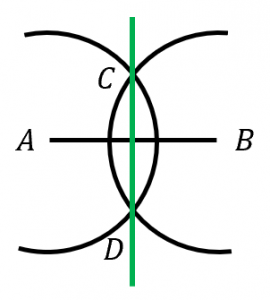
手順1と手順2で書いた2つの円の交点を $C,D$ とします。
2つの円は同じ半径なので、
$AC=AD=BC=BD$
が成立します。つまり、四角形 $ACBD$ は4つの辺の長さが全て等しいので、ひし形になります。
・ひし形は2本の対角線が垂直に交わります。つまり、$CD$ は $AB$ に垂直となります。
・ひし形は平行四辺形なので、対角線は中点で交わります。つまり、$CD$ は $AB$ の中点を通ります。
以上2つのことから、$CD$ は $AB$ の垂直二等分線になっていることが分かります。
垂直二等分線の練習問題
まず、適当に三角形 $ABC$ を書きます。
次に、$AB$ の垂直二等分線を作図します。
次に、$BC$ の垂直二等分線を作図します。
次に、$CA$ の垂直二等分線を作図します。
すると、うまく作図できていれば、3つの垂直二等分線は1点で交わります。
実際に作図して確認してみてください。
このように、どんな三角形に対しても、その3つの辺の垂直二等分線は1点で交わります。この点を三角形の外心と言います。
次回は 垂直二等分線の方程式の求め方を2通り解説 を解説します。
