四分位範囲と四分位偏差の意味

最終更新日 2019/03/31

データを小さい方から順に並べたとき
・下から $\dfrac{1}{4}$ の点、中央の点、上から $\dfrac{1}{4}$ の点を合わせて四分位数と言います。
・第3四分位数と第1四分位数の差を四分位範囲と言います。
・四分位範囲の半分のことを四分位偏差と言います。

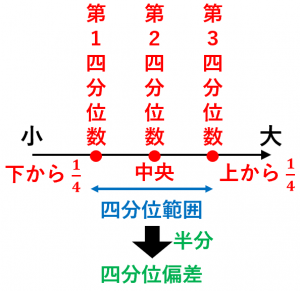
四分位数について復習してから、四分位範囲と四分位偏差について説明します。

四分位数とは

データを小さい方から順に並べたとき
・下から $\dfrac{1}{4}$ にある点を第1四分位数
・中央にある点を中央値（第2四分位数）
・上から $\dfrac{1}{4}$ の点を第3四分位数
と言います。

例えば、
10,20,30,40,50,70,90
という小さい順に並んだ7つのデータがあるとき、中央にある数字は40なので、第2四分位数は40です。

また、第1四分位数は「中央値を除いた左側のデータ (10,20,30) の中央値」と考える（場合が多い）ため、$20$ になります。

同様に、第3四分位数は $70$ になります。

四分位範囲は、第3四分位数と第1四分位数の差です。

四分位範囲は「データの真ん中50％部分の範囲（の広さ）」を表します。

例えば、
10,20,30,40,50,70,90
というデータの第1四分位数と第3四分位数はそれぞれ $20,70$ でした。よって、四分位範囲は、
$70-20=50$
となります。

四分位範囲は標準偏差や分散と同じく、データの散らばりを表す指標です。四分位範囲が大きいほど散らばりが大きいデータ（あるいは分布）と言えます。

そして、四分位範囲という指標は標準偏差や分散よりも外れ値に強いです。実際、四分位範囲は中央半分だけで決まるので、最大や最小付近のデータ値には依存しません。

また、四分位範囲は英語で Interquartile range と言うため、IQR と表されることがあります。

四分位偏差とは、四分位範囲の半分です。

第1四分位数を $Q_1$、第3四分位数を $Q_3$ と書くと、
四分位偏差は $\dfrac{Q_3-Q_1}{2}$ となります。

四分位偏差は、英語で Quartile Deviation または semi-interquartile range と言います。