上側確率、下側確率、両側確率、パーセント点という用語の意味についてそれぞれ説明します。
上側確率、下側確率
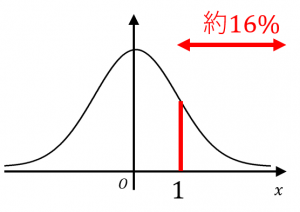
例えば、標準正規分布に従う確率変数 $X$ の値が $1$ より大きい確率は約 $16$%なので、
値 $1$ に対応する上側確率は $16$%となります。
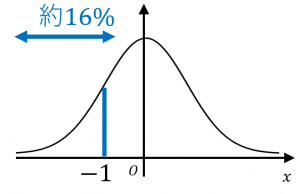
例えば、標準正規分布に従う確率変数 $X$ の値が $-1$ より小さい確率は約 $16$%なので、
値 $-1$ に対応する下側確率は $16$%となります。
両側確率
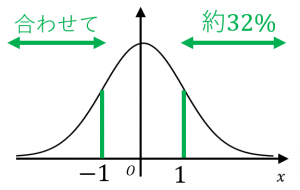
例えば、標準正規分布に従う確率変数 $X$ の絶対値が $1$ より大きい確率は約 $32$%なので、
絶対値 $1$ に対応する両側確率は $32$%となります。
※左右対称な分布の場合の説明です。左右対称でない分布の場合には、より一般に、
「確率変数が、ある値 $A$ より小さい、またはある値 $B$ より大きい確率」
のことを両側確率と言う場合があります。
パーセント点
・上側確率が $c$ であるような点のことを、上側 $c$ パーセント点と言います。
・下側確率が $c$ であるような点のことを、下側 $c$ パーセント点と言います。
・両側確率が $c$ であるような点のことを、両側 $c$ パーセント点と言います。
例えば、標準正規分布では、
上側 $5$%点は、約 $1.96$ です。
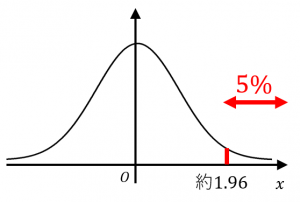
同様に、下側 $5$%点は、約 $-1.96$ です。
両側 $10$%点は、約 $1.96$ です。
・上側パーセント点、下側パーセント点、両側パーセント点は、いずれも単にパーセント点と呼ばれることがあります。
※上側確率、パーセント点などの定義に等号を含めるかどうか(このページでは含めないで定義しましたが)は、
・連続型確率分布の場合(特定の値を取る確率が、常に $0$ である場合)どちらの定義でも変わりません。
・離散型確率分布の場合、等号を含めるのかどうかを明確にしておく必要があります。
次回は Q-QプロットとP-Pプロットの意味と違い を解説します。
