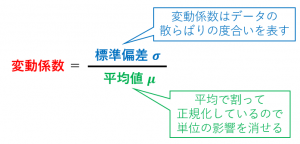
変動係数とは、標準偏差を平均で割ったもののことです。
変動係数の定義
変動係数は、$\dfrac{\sigma}{\mu}$、つまり標準偏差÷平均値で定義されます。
データの散らばり具合を表すのには標準偏差を使うことが多いですが、場合によっては標準偏差を平均で割って正規化した方がよいので、変動係数が使われます(具体例は後述)。
補足:平均と標準偏差の定義
データ $x_1,x_2,\cdots,x_n$ に対して、平均は、
$\mu=\dfrac{x_1+x_2+\cdots +x_n}{n}$
標準偏差は、
$\sigma=\sqrt{\dfrac{1}{n}\displaystyle\sum_{i=1}^n(x_i-\mu)^2}$
で定義されます。
(→平均の求め方(計算式)と意味、欠点)
変動係数をいつ使うか?
変動係数をどういうときに使えばよいのかを、具体例で確認してみます。
問題
3つのおかし:$90$円、$100$円、$110$円
3台のテレビ:$9$万円、$10$万円、$11$万円
値段の散らばり具合はどちらか大きいといえるか?
解答(標準偏差を用いた考え方)
データの散らばり具合を表す代表的な指標といえば、標準偏差です。そこで、それぞれ標準偏差を計算してみると、
おかし:$\sqrt{\dfrac{1}{3}\left\{(90-100)^2+(110-100)^2\right\}}$$=10\sqrt{\dfrac{2}{3}}$
テレビ:(同様に計算すると)$10000\sqrt{\dfrac{2}{3}}$
よって、標準偏差で比較すると、テレビのほうが1000倍散らばり具合が大きいことになります。
しかし、値段のスケールがそもそも全然違うので、テレビの方がおかしよりも標準偏差が大きくなるのは当然です。このように、標準偏差は、スケールが違う二つの量の散らばり具合を比較するのには不向きです。
解答(変動係数を用いた考え方)
そこで、変動係数(標準偏差を平均で割ることで、スケールの影響を消したもの)が使えます。この例について変動係数を計算してみます。
おかし:$10\sqrt{\dfrac{2}{3}}\div 100=\dfrac{1}{10}\sqrt{\dfrac{2}{3}}$
テレビ:$10000\sqrt{\dfrac{2}{3}}\div 100000=\dfrac{1}{10}\sqrt{\dfrac{2}{3}}$
となり、変動係数は同じです。つまり、変動係数で見れば散らばり具合は同じという結論になります。
このように、変動係数はスケールが違う二つの量の散らばり具合を比較するのに比較的向いています。
変動係数の性質
データを全部 $10$ 倍すると、標準偏差も平均も $10$ 倍されるので、変動係数は変わりません。このように、変動係数は定数倍の操作に対して不変です。
変動係数と標準偏差の比較
標準偏差:一つの量(データ)の散らばり具合を大雑把に把握するのに有効な指標です。
変動係数:二つの(スケールの異なる)量の散らばり具合を比較するのに有効な指標です。
次回は 情報量とエントロピーに関する重要用語の整理 を解説します。
