最小二乗法と最尤法の関係

最小二乗法＝等分散ガウス分布＋最尤推定
であることについて説明します。

最小二乗法とは

$n$ 個のデータ $(x_i,y_i)\:(i=1,\dots,n)$ が与えられた状況を考えます。

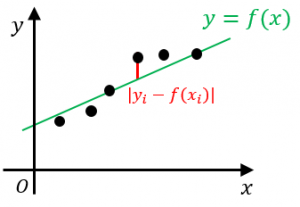
関数 $f(x)$ についての二乗誤差は、
$E=\displaystyle\sum_{i}\{y_i-f(x_i)\}^2$
と表現できます。

$f(x)$ としては何でも許すのではなく、予め関数の形に制限をもうけます。
例えば、直線 $f(x)=ax+b$ の中で、$E$ を最小にするようなものを求める、という定式化を使うことが多いです。この場合、$E$ を最小にするパラメータ $a$、$b$ を計算することになります。

ガウス分布＋最尤推定

先ほどと同じく、$n$ 個のデータ $(x_i,y_i)\:(i=1,\dots,n)$ が与えられた状況を考えます。

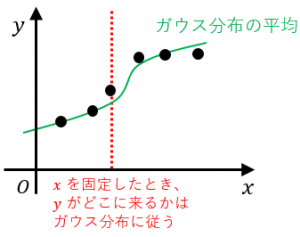
すなわち、説明変数 $x_i$ を固定したときに、目的変数 $y_i$ は、
$p(y_i)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(y_i-f(x_i)^2)}{2\sigma^2}\right\}$
というガウス分布に従って定まるものとします。

$f(x_i)$ は、ガウス分布の平均です。$x_i$ に依存するものとします。
$\sigma^2$ は、ガウス分布の分散で、$x_i$ によらず一定とします（等分散）。

対数尤度関数は、
$\log\displaystyle\prod_{i}p(y_i)\\
=\displaystyle\sum_{i}\log p(y_i)\\
=C-\dfrac{1}{2\sigma^2}\displaystyle\sum_{i}(y_i-f(x_i))^2$
となります。$C$ は平均 $f(x_i)$ によらない定数です。

つまり、尤度を最大にするような平均 $f(x_i)$ は、
$E=\displaystyle\sum_{i}(y_i-f(x_i))^2$ を最小にするようなものとなります。

２つの考え方の関係

最小二乗法というのはあくまでも一つの考え方に過ぎません。一般的には、最小三乗法や最小四乗法ではなく最小二乗法が優れているのだ、と主張することはできません。

しかし、データが等分散ガウス分布に従っている、と仮定できるときには（最小二乗法は最尤推定と同じ結果を導くので）最尤推定という手法によって、最小二乗法の正当性が指示される、と言えます。

次回は 共役事前分布の意味といくつかの例 を解説します。