正四面体の展開図2種類の書き方と組み立て方

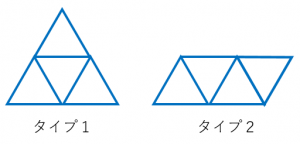
正四面体の展開図の書き方

正四面体の展開図は同じサイズの正三角形４枚からなります。

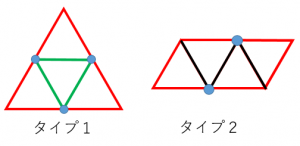
・タイプ１の場合、
大きな正三角形を書いて
各辺の中点を書いて
中点を結ぶ小さな正三角形を書く
ときれいな展開図が書けます。

・タイプ２の場合、
正三角形を４つ横につなげるだけですが、
外枠が平行四辺形になること
上の辺と下の点の中点が分岐点になっていること
を意識して書くと、きれいな展開図が書けます。

展開図の組み立て方

対応する辺（組み立てるときに接着する辺）に同じ番号をつけてみました。

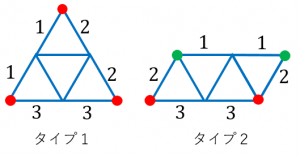
・それぞれ３つの辺を接着します。
・タイプ１の方がタイプ２より分かりやすいです。タイプ２の組み立て方もイメージできるとよいでしょう。

また、タイプ１では、端っこの赤い３つの頂点は組み立てたときに一致します。
タイプ２では、赤い２つの頂点、緑の２つの頂点が、組み立てたときにそれぞれ一致します。

なお、実際に模型を作ってみれば組み立て方は一目瞭然です。しかし、それぞれの組み立て方をイメージできると、展開図に関する問題を楽に解くことができます。

補足：上記の図から分かる別のこと
・正四面体の面の数が４つであることが分かります。
・正四面体の辺の数が６本であることが分かります。どちらの展開図も、辺の数は９本ですが、３組くっつけるので、組み立てた正四面体の辺の数は $9-3=6$ 本になります。
・正四面体の頂点の数が４つであることが分かります。どちらの展開図も頂点の数は６つですが、組み立てるときに２つ減って４つになることが分かります。

関連：正多面体の辺の数と頂点の数の求め方

余談：正三角錐の展開図

正三角錐は、底面が正三角形で側面が全て合同な二等辺三角形であるような立体です。正四面体のは正三角錐の特殊なものです。

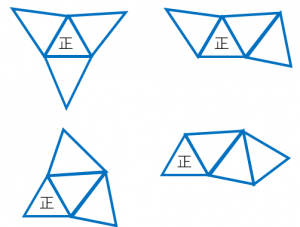
一般の正三角錐の展開図は、回転や裏返しで一致するものを除くと、図の４種類です。
正三角形には「正」と書いています。

それぞれの展開図を組み立てる様子を頭の中でイメージしてみてください。

次回は 立方体の展開図の一覧および面や辺の対応 を解説します。