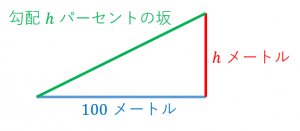
$100$ メートル水平に移動した時に高さが $h$ メートル上がる(または下がる)ような坂のことを勾配 $h$ パーセントの坂、と言います。勾配が大きいほど傾斜がきつい坂です。
坂道の勾配に関して、いろいろな量の計算の方法を説明します。
勾配を計算する
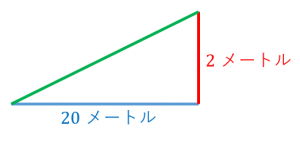
この坂道について、$100$ メートル水平に移動した時に、高さが $h$ メートル上がるとしましょう。すると、
$20:2=100:h$
となります。これを解くと、
$20h=200$
つまり、$h=10$ となります。
すなわち、勾配 $10$ パーセントの坂道です。
勾配から角度を計算する
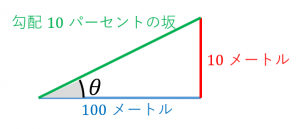
この角度を $\theta$ とおくと、タンジェントの定義より、
$\tan\theta=\dfrac{10}{100}=0.1$
になります。
これを、以下の方法のいずれかで求めると、$\theta\fallingdotseq 5.7^{\circ}$ になります。
・三角関数表を見る
・関数電卓などで $\mathrm{Arctan}\:0.1$ を計算する。
関連:arctanの意味、微分、不定積分
高さを計算する
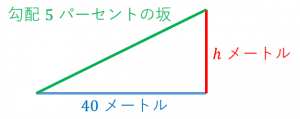
勾配 $5$ パーセントの坂を $100$ メートル水平方向に進むと $5$ メートル高くなります。
$40$ メートルは $100$ メートルの $\dfrac{40}{100}$ なので、$40$ メートル水平方向に移動した時に上がる高さは
$5\times\dfrac{40}{100}=2$
メートルとなります。
斜辺(斜めの距離)を計算する

$40$ メートル水平方向に移動した時に上がる高さは、先ほど計算したように、
$2$ メートルです。
よって、三平方の定理より、斜めの距離 を $l$ とすると、
$l^2=40^2+2^2$
です。計算していくと、
$l^2=1604$
$l\fallingdotseq 40.05$
つまり、斜めの距離は $40$ メートル $5$ センチくらいです。
ほぼ水平方向の距離と同じになります。
次回は 法面勾配の意味と、角度や距離の計算 を解説します。
