立体角の意味と計算の例

立体角とは

もうすこしきちんと立体角を定義すると、以下のようになります。

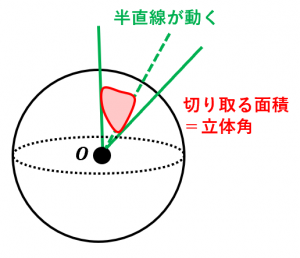
点 $O$ を端点とする半直線が動いてできる集合 $A$ に対し、$A$ が「点 $O$ を中心とする半径１の球」から切り取る面積を立体角と言います。

立体角の単位

立体角は、半径１の球（単位球）の一部の面積で定義されていました。単位球の表面積は $4\pi$ なので、立体角は、$0$ 以上 $4\pi$ 以下です。

「$4\pi$ ステラジアン」は「全方位」に対応する立体角です。

立体角の計算例

ただし、$\theta_0$ は円錐の中心軸と母線がなす角度（平面角）です。

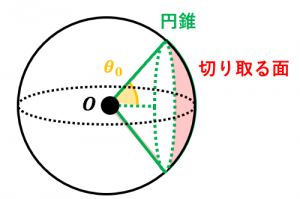
円錐の底面を円板をみなせば、「円板が張る立体角の公式」と言うこともできます。

円錐の立体角の公式を証明

放射の角度が $\theta$ の部分に対応する円は、半径が $\sin\theta$ なので、周の長さは、
$2\pi\sin\theta$
です。

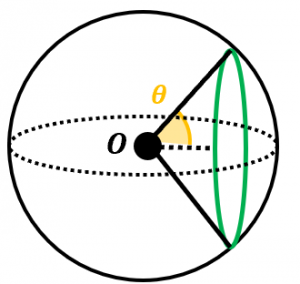
立体角は「$\theta=0$ の部分に対応する円」から「$\theta=\theta_0$ の部分に対応する円」までを集めたものの面積なので、
$\displaystyle\int_0^{\theta_0}2\pi\sin\theta d\theta\\
=2\pi(1-\cos\theta_0)$
となります。

ちなみに、この公式は「光の単位」を変換するときにも現れます。
カンデラ、ルーメン、ルクスの意味と変換

平面角との対応

三次元空間において、点 $O$ を端点とする半直線が動いてできる集合 $A$ に対し、$A$ が「点 $O$ を中心とする半径１の球」から切り取る面積が立体角（ステラジアン）

二次元平面において、点 $O$ を端点とする半直線が動いてできる集合 $A$ に対し、$A$ が「点 $O$ を中心とする半径１の円」から切り取る弧の長さが平面角（ラジアン）

並べてみると、平面角は立体角のきれいな拡張になっていることが分かります。

次回は arcsinの意味、微分、不定積分 を解説します。