最終更新日 2018/10/27
・一辺の長さが $a$ の立方体の対角線の長さは、$\sqrt{3}a$
・縦の長さ $a$、横の長さ $b$、高さが $c$ の直方体の対角線の長さは、$\sqrt{a^2+b^2+c^2}$
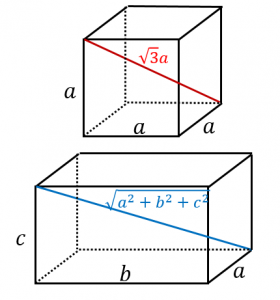
立方体の対角線の長さ
一辺の長さが $a$ である立方体の対角線 $AB$ の長さを計算してみます。
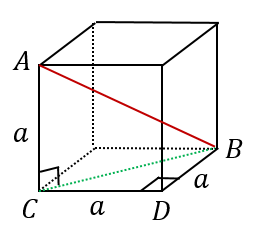
まず、三角形 $BCD$ は直角三角形なので、三平方の定理より、
$BC^2=CD^2+BD^2=2a^2$
さらに、三角形 $ABC$ も直角三角形なので、三平方の定理より、
$AB^2=AC^2+BC^2=a^2+2a^2=3a^2$
となります。両辺のルートを取ると、$AB=\sqrt{3}a$ となります。つまり、対角線の長さは一辺の長さの $\sqrt{3}\simeq 1.732$ 倍ということになります。
直方体の対角線の長さ
直方体の場合も、考え方は立方体の場合と全く同じです。
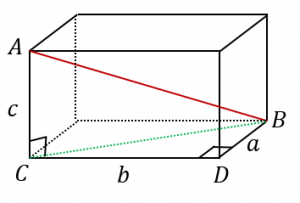
三角形 $BCD$ に三平方の定理を使うと、
$BC^2=a^2+b^2$
さらに、三角形 $ABC$ に三平方の定理を使うと、
$AB^2=BC^2+c^2=a^2+b^2+c^2$
となります。両辺のルートを取ると、$AB=\sqrt{a^2+b^2+c^2}$ となります。
この公式で $a=b=c$ すれば立方体の対角線の公式：$AB=\sqrt{3}a$ が導かれます。よって、直方体の公式だけ覚えればOKです。
立方体の対角線の長さを求める例題
例題
(1) 一辺の長さが $5\:\mathrm{cm}$ の立方体の対角線の長さを求めよ。
(2) 縦 $2\:\mathrm{cm}$、横 $3\:\mathrm{cm}$、高さ $6\:\mathrm{cm}$ の直方体の対角線の長さを求めよ。
解答
(1) 立方体の対角線の公式より、
$\sqrt{3}\times 5=5\sqrt{3}\:\mathrm{cm}$
(2) 直方体の対角線の公式より、
$\sqrt{2^2+3^2+6^2}\\
=\sqrt{4+9+36}\\
=\sqrt{49}\\
=7\:\mathrm{cm}$
次回は ねじれの位置の意味と直方体、三角柱、五角柱での例 を解説します。
