座標平面上で三角形の面積を計算する公式

座標平面上の３点 $(x_1,y_1),(x_2,y_2),(x_3,y_3)$ を頂点とする三角形の面積を計算する方法を説明します。

公式１：１つが原点である場合

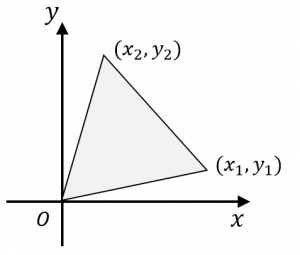
実際、座標平面上の３点 $(x_1,y_1),(x_2,y_2),(0,0)$ を頂点とする三角形の面積は、
$\dfrac{1}{2}|x_1y_2-x_2y_1|$
となります。
（この公式の証明はページの最後で説明します）

例えば、座標平面上の３点 $(1,2),(3,4),(0,0)$ を頂点とする三角形の面積は、
$\dfrac{1}{2}|1\times 4-3\times 2|\\
=\dfrac{1}{2}|4-6|\\
=1$
となります。

公式２：３つの頂点が原点でない場合

まず、３つの頂点を同じだけ平行移動しても、三角形の面積は変わりません。そこで、$x$ 方向に $-x_3$、$y$ 方向に $-y_3$ 平行移動させます。

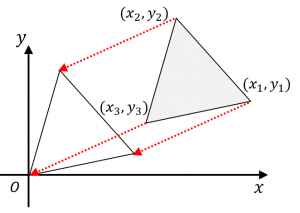
$(x_1,y_1)\to (x_1-x_3,y_1-y_3)$
$(x_2,y_2)\to (x_2-x_3,y_2-y_3)$
$(x_3,y_3)\to (0,0)$

すると、１つの頂点が原点に一致してくれます。そこで、先ほど紹介した公式を、平行移動した後の三角形に使うと、求める面積は
$\dfrac{1}{2}|(x_1-x_3)(y_2-y_3)-(x_2-x_3)(y_1-y_3)|$
となることが分かります。

解答１

青字の公式にそのまま当てはめると、面積は、
$\dfrac{1}{2}|(5-1)(4-2)-(3-1)(7-2)|\\
=\dfrac{1}{2}|4\cdot 2-2\cdot 5|\\
=\dfrac{1}{2}|8-10|\\
=2$
となります。

解答２

まず、$x$ 方向に $-1$、$y$ 方向に $-2$ 平行移動させます。
$(5,7)\to (4,5)$
$(3,4)\to (2,2)$
$(1,2)\to (0,0)$
そして、平行移動後の三角形に赤字の公式を使うと、面積は、
$\dfrac{1}{2}|4\times 2-2\times 5|\\
=1$
となります。

公式の証明

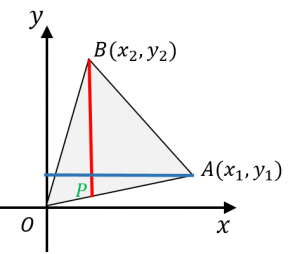
三角形 $OAB$ について、$BP$ を底辺とみなして考えます。
すると、三角形の面積は、
$B$ と $P$ の $y$ 座標の差
×
$O$ と $A$ の $x$ 座標の差
÷２
となります。

そこで、$P$ の $y$ 座標を計算してみましょう。まず、直線 $OA$ の方程式は、$y=\dfrac{y_1}{x_1}x$ です。
これに、$x=x_2$ を代入すると、$y=\dfrac{y_1}{x_1}x_2$
となります。

よって、三角形の面積は、
$|y_2-\dfrac{y_1}{x_1}x_2|$
×
$|x_1|$
÷２
$=\dfrac{1}{2}|x_1y_2-x_2y_1|$
となります。

※厳密には、上の証明では $x_1\neq 0$ であることが必要です。$x_1=0$ のときも公式が成立することは簡単に確認できます。

次回は 垂直二等分線の意味と作図方法を分かりやすく解説 を解説します。