ニューラルネットワークの仕組みと応用例を大雑把に解説します。
ニューラルネットワークとは
ニューラルネットワークは、すごく大雑把に言うと、複数の数字を入れたら複数の数字が返ってくるものです。数学の言葉を使えば、ニューラルネットワークとは、ただの多変数ベクトル値関数と言えます。
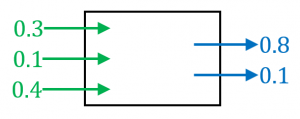
複数の数字を入れたら複数の数字が返ってくるブラックボックスのようなイメージを持っていただければOKです。ブラックボックスの中身は後ほど説明します。
応用例
ニューラルネットワークは、例えば、画像認識(犬と猫の写真を分類する問題)に使うことができます。
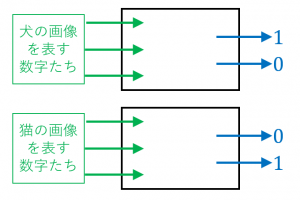
・画像は(各ピクセルの色味を数字で表現することで)複数の数字で表現することができます。
・犬の画像を入れたときには $(1,0)$ に近い値が返ってきて、猫の画像を入れたときには $(0,1)$ に近い値が返ってくるようなニューラルネットワークを作ることができれば、これを画像分類器として使うことができます。
・同様に、$k$ クラス分類問題(例えば、犬と猫と馬の画像を分類する問題は3クラス分類問題)は、出力が $k$ 個の数字であるようなニューラルネットワークを使って扱うことができます。
ニューラルネットワークの仕組み
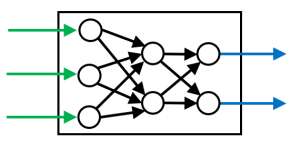
ブラックボックスの中身についてもう少し詳しく見てみましょう。
ニューラルネットワークは、パーセプトロンという比較的単純な関数を組合せたものです。
パーセプトロンは、複数の数字 $x_1,x_2,\dots,x_n$ に対して、1つの出力 $y$ を返す、以下のような関数です:
$y=f(w_1x_1+w_2x_2+\dots +w_nx_n)$
ただし、$w_1,\dots,w_n$ は重みパラメータで、$f$ は活性化関数という予め決められた単純な関数です。
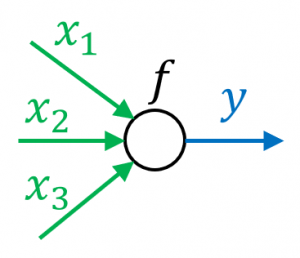
図のような丸で表現されることが多いです。
パーセプトロンの出力は単なる数字なので、次のパーセプトロンの入力として使うことができます。このように、複数のパーセプトロンを何層にも並べたものがニューラルネットワークです。
学習
この重みパラメータをうまく調整することで、目的の関数に近づけることを「学習」と言います。例えば、画像分類の例だと、犬と猫の大量の画像をもとに、重みパラメータを調整することで、
犬の画像を入れたときには $(1,0)$ に近い値が返ってきて、猫の画像を入れたときには $(0,1)$ に近い値が返ってくるという目的を達成するブラックボックスを作り出します。
ディープラーニングとは
パーセプトロンの層の数が多いニューラルネットワーク(を用いた学習手法)のことをディープラーニングと言います。
つまり、ディープラーニングとは、大雑把に言うと、単純な関数をたくさんつないで複雑な関数を表現できるようにしたもの(を用いた学習手法)と言えます。
次回は ウォード法によるクラスタリングのやり方 を解説します。
