クラスター分析の定番手法であるウォード法(Ward法)について説明します。
ウォード法とは
ウォード法は、凝集型階層的クラスタリングと呼ばれるクラスタリングの手法の1つです。
→クラス分類とクラスタリングの意味と違い
凝集型階層的クラスタリングとは、
1.全ての点が別々のクラスタである状態から始めて
2.「今あるクラスタの中で、最も距離が近い2つのクラスタを選んで1つのクラスタに合体する」という操作(図参照)を
3.目標のクラスタ数になるまで続ける
手法です。
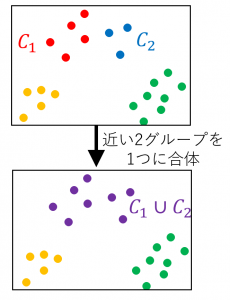
クラスタ間の距離の決め方によって最も距離が近い2つのクラスタは異なります。ウォード法では、後述の $d(C_1,C_2)$ を距離として使います。
ウォード法で使う距離
ウォード法において、2つのクラスタ $C_1$ と $C_2$ の間の距離は、
$d(C_1,C_2)=L(C_1\cup C_2)-L(C_1)-L(C_2)$
で定義されます。
ただし、$L(C)$ は、クラスタ $C$ 内での散らばり具合
を表します。ここで言う散らばり具合とは、重心からの距離の二乗和のことです。きちんと式で書くと、
$L(C)=\displaystyle\sum_{x\in C}D(x,g_C)^2$
です。($g_C$ は $C$ の重心で、$D(x,g_C)$ は $x$ と $g_C$ のユークリッド距離)
※ユークリッド距離とは、各成分の差の二乗和のルート(いわゆる普通の距離)のことです。
理由1:必ず$d\geq 0$ になります。
なぜ $d\geq 0$ になるのかは後述します。
理由2:ある意味で、2つのクラスタが似ているときほど $d$ が小さくなります。
理由2の感覚的な説明です:
2つのクラスタが似ている
$\iff$ 2つのクラスタを合体しても散らばり具合は増えない
$\iff$ 2つのクラスタを合体する前の散らばり具合 $L(C_1)+L(C_2)$ から、合体したあとの散らばり具合 $L(C_1\cup C_2)$ への増加量が小さい
$\iff$ $d$ が小さい
ウォード法の距離の別の姿
実は、$d(C_1,C_2)$ は、それぞれのクラスタの重心 $g_{C_1},g_{C_2}$ と、クラスタに属する点の数 $n_1,n_2$ を使って、
$d(C_1,C_2)=\dfrac{n_1n_2}{n_1+n_2}D(g_{C_1},g_{C_2})^2$
と表すこともできます。
この式は、重心の定義とウォード法における距離の定義を使って計算していくと導けます。
参考文献:Distances between Clustering
重心間のユークリッド距離を使ったきれいな式になっています。もともとの定義よりもシンプルです。
そして、
・この式を見れば、すぐに $d\geq 0$ であることも分かります。
・重心間の距離が同じでも、クラスタ数 $n_1,n_2$ が増えるほど、距離 $d(C_1,C_2)$ は大きくなります。よって、ウォード法において、メンバーの多いクラスタ同士は合体されにくくなります。
次回は 決定木、分類木、回帰木の意味と具体例 を解説します。
