三角形の内心の証明と頻出例題2問

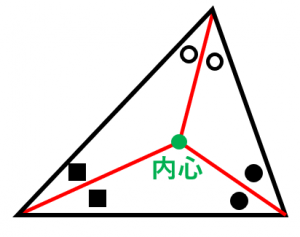
三角形の内心が存在することの証明や、三角形の内心に関する例題を解説します。

三角形の内心の証明

三角形の内心とは、3つの角の二等分線の交点です。三角形の内心が存在することを証明してみましょう。

$\angle A$ と $\angle B$ の二等分線の交点を $I$ とします。このとき $CI$ が $\angle C$ の二等分線になっていることを証明できればOKです。

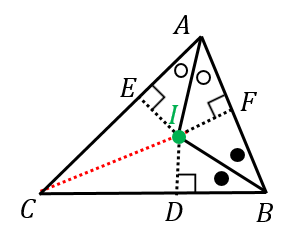
$I$ から各辺に垂線を下ろし、その足を $D,E,F$ とします。
三角形 $AIF$ と $AIE$ は（直角三角形で斜辺と他の1つの角がそれぞれ等しいので）合同です。よって、$IE=IF$ です。同様に、$ID=IF$ も分かります。
よって、$ID=IE$ です。

したがって、三角形 $CID$ と $CIE$ は（直角三角形で斜辺と他の1つの辺がそれぞれ等しいので）合同です。つまり、$CI$ は $\angle C$ の二等分線になっています。以上により、三角形の内心が存在することの証明が完了しました。

角度を求める問題

三角形の内心は、角の二等分線の交点なので、これを利用するといろいろな場所の角度を計算することができます。例題を解いてみましょう。

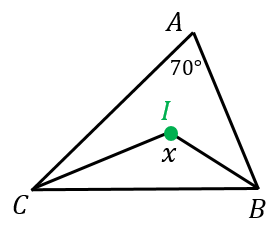
解答：
内心の性質より、$BI$ は角の二等分線なので、$\angle ABI=\angle CBI$
また、$CI$ も角の二等分線なので、$\angle ACI=\angle BCI$
よって、
$\angle ABC+\angle ACB=2(\angle CBI+\angle BCI)$

一方、$\angle A=70^{\circ}$ なので、
$\angle ABC+\angle ACB=180^{\circ}-70^{\circ}=110^{\circ}$

以上2つの結果から、
$\angle CBI+\angle BCI=\dfrac{1}{2}\cdot 110^{\circ}=55^{\circ}$

よって、三角形 $IBC$ の内角の和は $180^{\circ}$ なので、
$x+55^{\circ}=180^{\circ}$

よって、$x=125^{\circ}$

辺の比を求める問題

三角形の内心に関する問題の中でも、角の二等分線定理を使って辺の長さの比を計算する問題は頻出です。

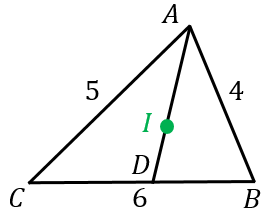
解答：
内心の性質より、$AI$ は角の二等分線なので、角の二等分線定理より
$BD:DC=AB:AC=4:5$
参考：角の二等分線定理（内角、外角それぞれ）

よって、$BD=\dfrac{4}{4+5}BC=\dfrac{4}{9}\times 6=\dfrac{8}{3}$

次に、$BI$ も角の二等分線なので、角の二等分線定理より
$AI:ID=AB:BD\\
=4:\dfrac{8}{3}\\
=12:8\\
=3:2$
となる。

次回は 「30°、60°、90°」と「45°、45°、90°」の直角三角形の辺の比 を解説します。