$n$ 角形の内角の和は、$180\times (n-2)$ 度
例えば、
三角形の内角の和は、$180\times (3-2)=180^{\circ}$
四角形の内角の和は、$180\times (4-2)=360^{\circ}$
五角形の内角の和は、$180\times (5-2)=540^{\circ}$
六角形の内角の和は、$180\times (6-2)=720^{\circ}$
です。
証明1:三角形に分割する
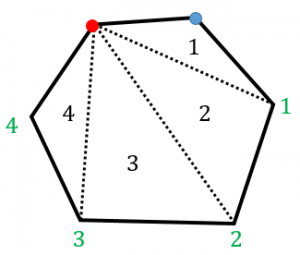
図のように $n$ 角形の1つの頂点から、対角線をたくさん引くことによって、$n$ 角形を $(n-2)$ 個の三角形に分割することができます。図は $n=6$ の場合で、三角形は4つです。

→注目した頂点とその右どなりの頂点以外の頂点は $(n-2)$ 個ありますが、それぞれに三角形1つを対応させることができるので、三角形の数は $(n-2)$ 個です。
三角形の内角の和は $180^{\circ}$ なので、
$n$ 角形の内角の和は、三角形 $(n-2)$ 個ぶん、つまり、
$180\times (n-2)^{\circ}$ となります。
証明2:中心に点をうつ
図のように $n$ 角形の中央付近に点を打ち、頂点全てと線で結びます。すると、三角形が $n$ 個できます。

この三角形の内角の和を全て足しあげると、
$180\times n$ となります。
しかし、この計算には、中央の一周ぶんの余分な角度も含まれているので、$360^{\circ}$ を引く必要があります。
結局、$n$ 角形の内角の和は、
$180n-360=180(n-2)^{\circ}$
となります。
証明3:数学的帰納法
三角形の内角の和が $180^{\circ}$ であることは認めてしまいます。
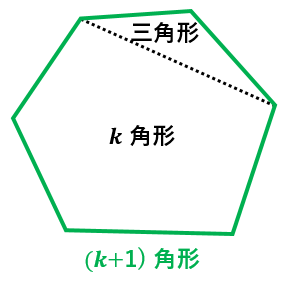
$k$ 角形の内角の和が $180(k-2)^{\circ}$ だと仮定すると、
$(k+1)$ 角形の内角の和は、
(図のように $k$ 角形と三角形に分割できるので)
$180(k-2)+180=180\{(k+1)-2\}$
となります。
つまり、$k$ 角形で公式が正しければ、$(k+1)$ 角形でも公式が正しいことが分かりました。よって、数学的帰納法により、公式が証明されました。
関連
四角形の場合は、平行線の錯角を使ったおもしろい証明方法もあります。
→四角形の内角の和が360°であることの2通りの証明
この公式を使って、正多角形の内角と外角の大きさを求めることができます。
→正多角形の内角と外角の大きさ
