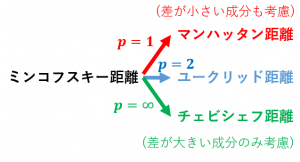
ミンコフスキー距離と、その特殊な場合であるユークリッド距離、チェビシェフ距離、マンハッタン距離について解説します。
ミンコフスキー距離とは
2つのベクトル $\overrightarrow{x}=(x_1,x_2,\dots,x_n)$、$\overrightarrow{y}=(y_1,y_2,\dots,y_n)$ がどれくらい離れているかを表す量がいくつかあります。
その中で、
$\left(\displaystyle\sum_{k=1}^n|x_k-y_k|^{p}\right)^{\frac{1}{p}}$
をミンコフスキー距離と言います。
ただし、$p$ は $1$ より大きい数(パラメータ)とします。
ユークリッド距離
ミンコフスキー距離で $p=2$ とすると、
$\sqrt{\displaystyle\sum_{k=1}^n(x_k-y_k)^{2}}$
となります。
「各成分の差の二乗和のルート」という、よく見る普通の距離です。
参考:ユークリッド空間の意味を分かりやすく説明する
マンハッタン距離
ミンコフスキー距離で $p=1$ とすると、
$\displaystyle\sum_{k=1}^n|x_k-y_k|$
となります。
「各成分の差の絶対値の和」です。ユークリッド距離の次に有名な距離ではないでしょうか。
チェビシェフ距離
チェビシェフ距離は、
$\displaystyle\max_{k}|x_k-y_k|$
で定義されます。最も離れている成分についての差の絶対値です。
これを導出してみます。
$|x_k-y_k|$ が最大となるような $k$ を $k_0$ と書くと、
$\left(\displaystyle\sum_{k=1}^n|x_k-y_k|^{p}\right)^{\frac{1}{p}}\\
=|x_{k_0}-y_{k_0}|\left(\displaystyle\sum_{k=1}^n\dfrac{|x_k-y_k|^{p}}{|x_{k_0}-y_{k_0}|^p}\right)^{\frac{1}{p}}$
と変形できますが、和の各項は全て $1$ 以下で、$k=k_0$ のときには $1$ なので、
和を $\dfrac{1}{p}$ 乗したものは $p\to\infty$ で $1$ に近づいていきます。
つまり、$p\to\infty$ で、ミンコフスキー距離は $|x_{k_0}-y_{k_0}|$ に収束します。
各距離の性質
・$p=1$ のマンハッタン距離は「どの成分も平等に見る」
・$p=\infty$ のチェビシェフ距離は「差が一番大きい成分以外は完全無視する」
・$p=2$ のユークリッド距離はその中間くらい
と言えます。
三角不等式
つまり、$D_p(\overrightarrow{x},\overrightarrow{y})=\left(\displaystyle\sum_{k=1}^n|x_k-y_k|^{p}\right)^{\frac{1}{p}}$
とおくと、全ての $\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}$ に対して
$D_p(\overrightarrow{x},\overrightarrow{y})+D_p(\overrightarrow{y},\overrightarrow{z})\geq D_p(\overrightarrow{x},\overrightarrow{z})$
が成立します。
これをミンコフスキーの不等式と言うことがあります。
次回は マハラノビス距離の意味を2次元の場合で理解する を解説します。
