マハラノビス距離の意味を２次元の場合で理解する

マハラノビス距離とは

赤い点のデータ群があるときに、青い点と緑の点はどちらがデータ群から離れているでしょうか？

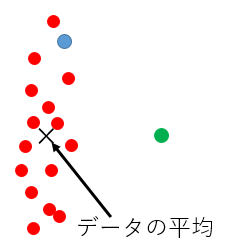
平均からの「普通の」距離（ユークリッド距離）を考えると、両者は同じくらい平均から離れているように見えますが、緑の点の方が「赤いデータ群から離れている」と考えるのが自然ではないでしょうか？

つまり、データの各方向への散らばり具合まで考慮した「データ群からの距離」を考える必要があります。これを実現するのがマハラノビス距離です。

具体的には、平均ベクトルが $\overrightarrow{\mu}$ で、分散共分散行列が $\Sigma$ であるようなデータ群があるとします（$\Sigma$ は正則とします）。このとき、データ $\overrightarrow{x}$ がデータ群からどれくらい離れているかを表す量として、マハラノビス距離が、
$d=\sqrt{(\overrightarrow{x}-\overrightarrow{\mu})^{\top}\Sigma^{-1}(\overrightarrow{x}-\overrightarrow{\mu})}$
と定義されます。

マハラノビス距離を使うことで「データの異常度」を定量化することができるため、異常検知などに使えます。

マハラノビス距離の性質

・マハラノビス距離はスカラーです。
$(\overrightarrow{x}-\overrightarrow{\mu})^{\top}\Sigma^{-1}(\overrightarrow{x}-\overrightarrow{\mu})$ はスカラー（二次形式）だからです。

・$\overrightarrow{x}$ が平均ベクトル $\overrightarrow{\mu}$ と一致するときには、マハラノビス距離は $0$ になります。

・$\Sigma^{-1}$ は正定値対称行列なので、$\overrightarrow{x}$ が $\overrightarrow{\mu}$ と一致しないときにはマハラノビス距離は $0$ より大きくなります。

・マハラノビス距離は、多変量正規分布の密度関数の指数の肩に非常に似ています。
（平均がデータ群の平均と等しく、共分散行列がデータ群の共分散行列と等しいような多変量正規分布の密度関数について考えることで）
マハラノビス距離が大きい
→その点での確率密度が小さい
→異常度が高い
と解釈することができます。

一次元の場合

一次元データの場合、

平均ベクトルはスカラー $\mu$
分散共分散行列も単なるスカラー（データの分散 $\sigma^2$）になります。

よって、マハラノビス距離は、
$d=\sqrt{(x-\mu)\cdot\dfrac{1}{\sigma^2}\cdot (x-\mu)}$
$=\dfrac{|x-\mu|}{\sigma}$
となります。

これは、平均からの差を標準偏差 $\sigma$ で正規化したような形になっています。

絶対値を除いたもの $\dfrac{x-\mu}{\sigma}$ は $z$ スコアという名前で知られています。
統計における標準化の意味と目的

二次元の場合

二次元の場合のマハラノビス距離を具体的に書き下してみます。

$\overrightarrow{x}=\begin{pmatrix}x_1\\x_2\end{pmatrix}$、$\overrightarrow{\mu}=\begin{pmatrix}\mu_1\\\mu_2\end{pmatrix}$、$\Sigma=\begin{pmatrix}\sigma_1^2&\sigma_{12}\\\sigma_{12}&\sigma_2^2\end{pmatrix}$
とします。

このとき、相関係数を $\rho=\dfrac{\sigma_{12}}{\sigma_1\sigma_2}$ とすると、
$\Sigma^{-1}=\dfrac{1}{\sigma_1^2\sigma_2^2-\sigma_{12}^2}\begin{pmatrix}\sigma_2^2&-\sigma_{12}\\-\sigma_{12}&\sigma_1^2\end{pmatrix}\\
=\dfrac{1}{1-\rho^2}\begin{pmatrix}\frac{1}{\sigma_1^2}&-\frac{\rho}{\sigma_1\sigma_2}\\-\frac{\rho}{\sigma_1\sigma_2}&\frac{1}{\sigma_2^2}\end{pmatrix}$

なので、マハラノビス距離は、
$\sqrt{\dfrac{\frac{(x_1-\mu_1)^2}{\sigma_1^2}-\frac{2\rho(x_1-\mu_1)(x_2-\mu_2)}{\sigma_1\sigma_2}+\frac{(x_2-\mu_2)^2}{\sigma_2^2}}{1-\rho^2}}$
となります。

分散が大きい方向の影響度は小さく、分散が小さい方向への平均からのズレは強く影響することが分かります。

次回は ハフ変換の意味と例を分かりやすく解説 を解説します。